基于威布爾參數(shù)的風(fēng)功率密度估算
在做風(fēng)資源分析中,因沒(méi)有測(cè)風(fēng)數(shù)據(jù)常常會(huì)遇到這種情況,知道該地的平均風(fēng)速,卻不知道平均風(fēng)功率密度。平均風(fēng)功率密度并不是由平均風(fēng)速直接計(jì)算而來(lái),由此會(huì)給資源分析師們帶來(lái)一些不便。為此小編通過(guò)威布爾參數(shù)的方法結(jié)合現(xiàn)有的計(jì)算成果和自己的分析計(jì)算來(lái)確定一個(gè)簡(jiǎn)便的風(fēng)功率估算方法。
風(fēng)功率分布參數(shù)的確定
根據(jù)風(fēng)功率密度的定義,風(fēng)功率密度P為空氣密度ρ和風(fēng)速v兩個(gè)變量的函數(shù)。對(duì)某一地區(qū)而言,空氣密度變化不大,可忽略不計(jì),因此風(fēng)功率密度主要由v3的變化決定。由此可以認(rèn)為,風(fēng)能的概率分布取決于風(fēng)速的概率分布特征。經(jīng)推算:
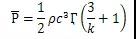
K、c為風(fēng)速分布的威布爾參數(shù)
可見(jiàn)風(fēng)能的分布仍是威布爾分布,形狀參數(shù)變?yōu)?/k,尺度參數(shù)變?yōu)閏3。
尺度參數(shù)c的優(yōu)化
根據(jù)平均風(fēng)速和最大風(fēng)速估計(jì)威布爾參數(shù)的方法可以得出
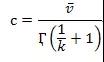
所以尺度參數(shù)c可以省略不考慮。
形狀參數(shù)k的優(yōu)化
根據(jù)經(jīng)驗(yàn),風(fēng)速分布的形狀參數(shù)k值變化范圍在1.0~3.0之間,3/k的范圍在1.0~3.0之間。伽馬函數(shù)表中,x變量的取值范圍為1.000~1.999。
根據(jù)伽馬函數(shù)關(guān)系式

通過(guò)觀察伽馬函數(shù)表發(fā)現(xiàn),函數(shù)值的變化幅度不大,因此當(dāng)x-1取值為1.0~1.999時(shí),函數(shù)可取近似值0.9。
最終優(yōu)化結(jié)果
綜合以上結(jié)論,最終的風(fēng)功率函數(shù)可以估算為以下公式:

n取值為0、1或2,取決于伽馬函數(shù)(x-1)的迭代次數(shù)。
通過(guò)上公式發(fā)現(xiàn)平均風(fēng)功率之和平均風(fēng)速、形狀參數(shù)有關(guān)。根據(jù)經(jīng)驗(yàn)得知形狀參數(shù)在小片內(nèi)變化不明顯,且在本式中影響較小,所以可有該地區(qū)的平均值2.34代替:
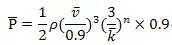
下表為在某中尺度平臺(tái)上選取的五個(gè)點(diǎn)

圖中五個(gè)點(diǎn)距離范圍為5km~15km,風(fēng)功率一欄為觀測(cè)到數(shù)值,估算風(fēng)功率一欄為取k平均值2.34后計(jì)算結(jié)果。從兩列數(shù)據(jù)結(jié)果來(lái)看,因k值影響較小,在一定范圍內(nèi),此估算方法具有一定的參考價(jià)值。

責(zé)任編輯:小琴
- 相關(guān)閱讀
- 火力發(fā)電
- 風(fēng)力發(fā)電
- 水力發(fā)電
- 光伏太陽(yáng)能