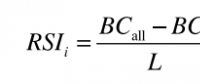第二節 電力企業的資金分析

一、資金的時間價值

作為電力企業的決策人員來說，在商品經濟分析中應建立一個重要的概念：貨幣具有時間價值。所謂貨幣的時間價值就是貨幣在流通過程中所產生的新的價值。

資金的時間價值的具體表現就是利潤和利息。利潤是指對投資過程而言的，利息是指對借貸而言的。例如，年初從銀行貸款100萬元，年利率為10%，明年初應償還110萬元，后年初就應償還121萬元。如此，10萬元和21萬元就是100萬元資金的一年和二年的時間價值。

1.利息

利息是借款人支付給貸款人的報酬。當電力企業向國家銀行取得貸款時，利息則是企業支付給銀行的一部分純收入，以有列于節約使用資金，促進資金周轉，加強經濟核算和增加積累;而企業向銀行存款時，銀行對電力企業也付一定的利息，其目的在于鼓勵節約，使閑置資金用于國家建設。

利息分單利和復利兩種，所謂單利只按本金計算利息，累計起來的利息不再計利。例如借款100元，借期3年，每年按10%標準還利，則第3年未應付本利和為loo+loo×0-1×3-130(元)。而復利是不僅本金要逐期還息，每期累計起來的利息也要計息，如前例，第三年末按復利計算應還的本利和應為：

第一年末 100+100×0.1=110(元)

第二年末 110+110×0.1=121(元)

第三年末 121+121×0.1=133.1(元)

這比用單利法多計利息3.1元。在計算貨幣的時間價值時皆采用復利法。

2.利率

利率系指一定時期內利息額與貸出金額的比率，即

利率有年利率，月利率和日利率之分，是根據國家客觀經濟條件有計劃規定的。

3.名義利率

名義利率是掛名的、非有效利率，時間是以一年為基礎，每年只計息一次的利率，用r

表示。

名義利率一周期利率×每年復利周期數

例如，存款100元，計息周期為3個月，每個利息期的利率為3%，則年利率為12%。此處，12%為名義利率，而3%為周期利率，即

r=3%×4=12%

4.周期利率

它是將名義利率按同等標準分n次計息，即

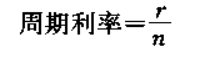
5.實際利率

實際利率是按每年計息期數復利計息所得的利率，實際利率是有效利率。這就是說，若以周期利率計算年利率，并考慮資金的時間價值，這時的年利率便是實際利率。

通常所說的年利率都是指名義利率，如不對計息時間加以說明，則表示一年計息一次，這時名義利率等于實際利率。例如，名義利率為6%，每年計息一次，實際利率也是6%。若計息期短于一年，例如可按半年、季，月、周計息，則每年計息次數為2、4、1 2、52次。計息次數越多，實際利率比名義利率越高。就前例而言

本利和=100 *(1+0* 03)2 =106. 09(元)

利息=106.09-100=6.09(元)

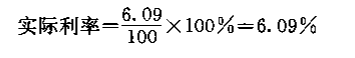
因此，實際利率力6.09%，大于名義利率6“由

由此可見：①名義利率對資金的時間價值反映得不夠完全;②實際利率反映資金的時間價值;③計息周期越短，實際利率與名義利率的差值越大。

如設i為實際利率.r為名義利率，訂為計息期數，P為年初投資現值，F為本利和，則

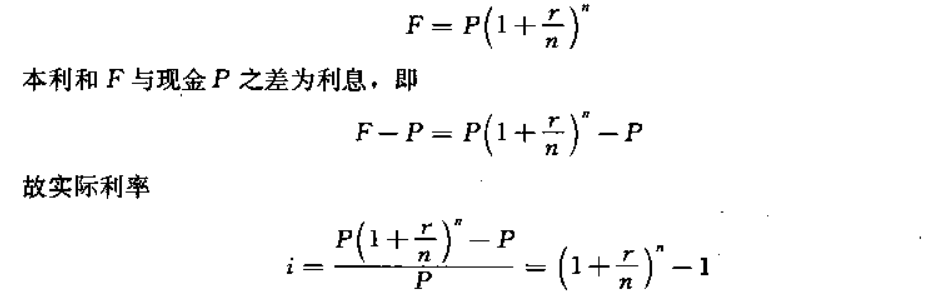
三、投資現值的折算

投資的折算有兩種方法：其一是分期復利法;其二是瞬間復利法。

1.分期復利法折算投資的現值

設期初一次性投入資金的現值為P元，每期利率為i，期末所獲得利息為Pi，那么，期末的本利和為

2.用分期復利法折算s為現價P的公式

上述兩個例子表明：①100萬元的投資.5年來的差額為61. 051萬元，這就是100萬元的貨幣在5年內所產生的時間價值;②5年后的100萬元，如果年利率為10%，只與現在的62. 092萬元相當。

這就是說，如將100萬元的資金積壓5年，則要損失掉61. 051萬元。如果購買100萬元的設備。5年不用，即使5年后該設備尚值100萬元，也只相當現在的62. 092萬元，丟掉了37. 908萬元。因此，在企業經營中積壓資金和購置閑置設備是極不合算的。

3.年金的分期復利公式

假定初投資的現價為P，要求在n年內等額回收，則每年的回收額則稱為年金M。這里要解決的問題是：投資的現價P和年金M的換算關系。

如設年金為M，年利率為i，則第一年末回收M的現價為

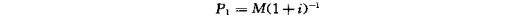
4.本利和與年金換算的分期復利公式

四、利息的計算

1.間斷復利息的計算

2.連續復利息計算公式