摘要

針對電力市場均衡策略的求解,現階段國內外廣泛采用非線性互補算法和循環迭代的方法。其中,非線性互補算法是通過Karush-Kuhn-Tucker條件將發電商最優反應函數轉換成一組半光滑非線性互補方程組,松弛因子維度高且算法異常復雜。而循環迭代法采用重復求解各發電商的最優反應函數的思想,常常因為收斂性差而求不到均衡解。針對上述問題,提出了一種基于雙層粒子群算法求解市場均衡的思路。其中,外層粒子群算法搜索可行域內的策略組合,以提出的納什適應度函數為尋優標準;內層粒子群算法和內點法結合計算外層中的納什適應度函數值。采用標準3節點和IEEE 30節點測試系統對所提算法進行了仿真,求得結果與采用非線性互補算法的結果完全一致,驗證了所提出的雙層粒子群算法的有效性。

0 引言

納什均衡是預測和分析電力市場走向的有效工具,對市場的設計及監管具有重要意義[1]。一直以來,求解電力市場均衡是一個十分復雜的問題。經典的古諾均衡[2-3]和供給函數均衡[4-5]解析計算方法,由于沒有考慮網絡阻塞、出力約束等,無法適應于實際電力市場均衡計算,因此需要探索有效的方法求解電力市場均衡問題。

關于電力市場均衡的求解算法,國內外學者做了許多研究。文獻[6-7]運用窮舉法獲取發電商的最優反應函數以探討市場古諾均衡。文獻[8]利用迭代的方法求解納什均衡,但常常因為收斂性差而求不到均衡解;文獻[9-11]利用Karush-Kuhn-Tucker條件,將發電商的雙層優化問題轉換成一組半光滑非線性互補方程組,但是算法轉化過程及半光滑方程組的求解過程異常復雜,中間松弛變量維數高;文獻[12-15]將發電商競價的均衡問題模擬成種群協同進化的過程,采用協同進化算法求解,但發電商某策略下的收益是隨對手策略變化的,單純將發電商的收益作為評估策略的適應度,理論可靠性有待商榷;文獻[16-17]運用多項式方程系統算法求解市場存在的混合策略均衡,當策略離散度高時求解時間也等比增加,且需要對結果進行驗證,不適合進行大規模求解計算。文獻[18]用多智能體仿真系統 (agent-based modeling of electricity systems,AMES)模擬市場均衡,可仿真的結果并未收斂至納什均衡解。由此,本文提出了一種基于雙層粒子群算法(particle swarm optimization,PSO)求解電力市場均衡的新思路。

針對求解電力市場均衡的復雜問題,本文從納什均衡的理論出發,提出了納什適應度函數用以評價策略組合是否為納什均衡,并采用雙層粒子群算法進行均衡策略的進化求解。最后,采用標準3節點測試系統和IEEE 30節點測試系統對本文所提算法進行了仿真分析,仿真結果與用非線性互補算法求得的結果完全一致,驗證了本文提出的雙層粒子群算法的有效性。

1 電力市場運營模式

電力市場采用暗標拍賣的機制,發電商各自提交報價策略,獨立系統運營商(independent system operator,ISO)在滿足系統運行約束的條件下,按照最大化社會福利進行市場出清。

1.1 發電商供給函數模型

本文采用線性供給函數(linear supply function,LSF)模型構建發電商的報價策略,單位時間內,發電商的成本函數可以表示為出力的二次函數：

1.2 負荷需求模型

與發電商報價函數對應,負荷逆需求函數反映了用戶意愿接受的用電價格與用電量的關系。

2 電力市場納什均衡模型

2.1 納什均衡基礎

納什適應度函數fnash取得最大值n,納什均衡是該適應度函數的全局最優點。

由此,可以運用粒子群算法搜索策略組合域{S1,S2,?,Sn}內的所有取值組合,計算其納什適應度函數值,直到搜索得到適應度最大的策略組合。所以,求解納什均衡的關鍵在于計算納什適應度函數值。納什適應度函數的分子部分是發電商收益,通過計算ISO的出清問題(式(6)(7))便可求得;分母部分則是發電商在已知對手策略情況下最大化自身收益的雙層優化模型。下面討論求解發電商競價的雙層優化模型。

2.3 發電商競價的雙層優化模型

發電商在已知對手策略情況下最大化自身收益是一個雙層優化模型。下層是ISO市場出清問題,將節點電價、發電商中標出力返回上層;上層是發電商在策略約束下最大化收益問題。

本文采用粒子群和內點法求解發電商競價的雙層優化問題[20]。發電商競價的雙層優化問題,已有大量文獻對其進行不同的求解分析,一般稱為上下層。而本文提出的雙層粒子群算法也是一個雙層優化問題,為與上述叫法區分開,稱為內外層。

3 求解算法

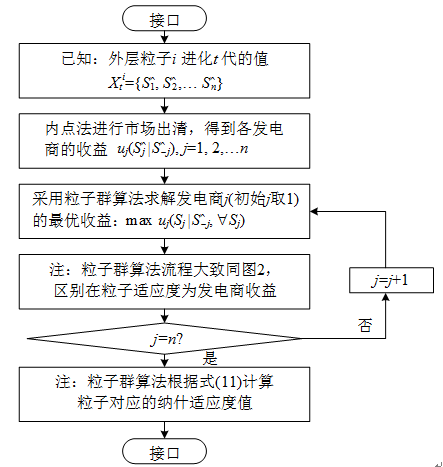
本文運用雙層粒子群算法求解電力市場均衡,算法思路如圖1所示。其中,外層采用粒子群算法搜索可行域內的所有策略組合,計算其納什適應度值,以此判斷其是否為納什均衡;而計算策略組合的納什適應度值屬于內層問題,需要求解“發電商競價的雙層優化問題”(這是一個上下層問題,見2.3節)方能解決,內層采用粒子群算法和內點法結合求解“發電商競價的雙層優化問題”。通過內外層的配合,從而整個市場均衡問題通過兩層粒子群

算法得到了解決。

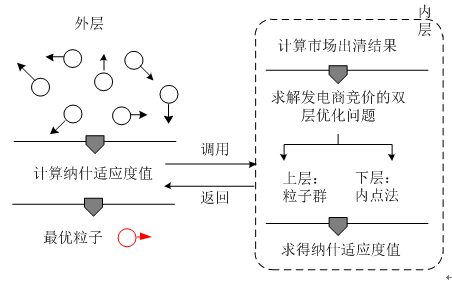
3.1 外層粒子群算法搜索策略組合

采用粒子群算法搜索發電商的策略組合,以納什適應度函數評價解的品質,求解流程如圖2所示。

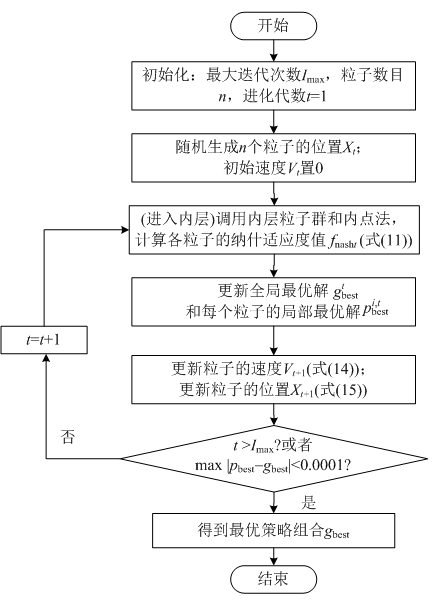
3.2 內層粒子群和內點法求解納什適應度函數

采用粒子群和內點法[21-22]求解各發電商最大化收益的雙層優化模型,套用式(11),便可得到組合策略XitXti對應的納什適應度函數值,具體求解流程如圖3所示。其中,內層粒子群算法流程與圖2類似,此處不再贅述,區別在于粒子適應度為發電商收益,粒子位置為單個發電商策略。

3.3 算法分析

1)采用粒子群算法搜索均衡解,規避了求解發電商雙層優化構成的半光滑非線性方程組,在保證結果準確的前提下,以時間代價換取算法簡化。

2)求解時間長是粒子群這類智能算法避免不了的問題,但由于其可并行計算的特性,可以采用matlab并行計算函數parfor進行多線程計算,從而大大減小求解時間。

3)可能存在內層粒子群搜索不徹底造成納什適應度函數值偏大的情況,但文獻[20]和多次重復仿真結果表明,內層粒子群的一維搜索能力可以媲美全局最優。

4 算例分析

4.1 3節點測試系統

為了驗證雙層粒子群算法的有效性,本節運用雙層粒子群算法求解文獻[9-10]的3節點測試系統,并將求解結果進行比對。3節點系統網絡拓撲和基本參數如圖4和表1所示,各節點間由相同導納的線路相連,線路1-2的輸電上限為Lmax。

考慮兩種情況,一種為無輸電阻塞(Lmax= 500 MW)的情形,另一種為有輸電阻塞(Lmax= 25 MW)的情形。

仿真參數設置：外層粒子群,粒子數目10,最大進化代數200;內層粒子群,粒子數目12,最大進化代數200;kmin,kmax分別取1和2。

1)情形1,無輸電阻塞Lmax=500 MW。

最優粒子的位置和納什適應度值變化情況如圖5所示,左軸是策略組合系數,右軸是策略組合的納什適應度值。隨著進化代數增加,最優粒子的納什適應度值越來越大,最終趨近2.0達到收斂,策略組合收斂至(1.1343;1.0825),此結果與文獻[9-10]中用非線性互補算法求得的結果完全一致,說明了本文提出算法的有效性。

2)情形2,有輸電阻塞Lmax=25 MW。

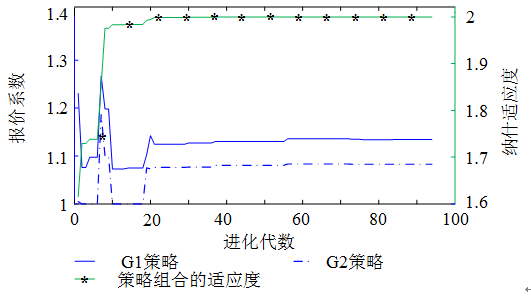
在有輸電阻塞下,進化過程中最優粒子的位置和納什適應度值變化情況如圖6所示。隨著進化代數增加,最優粒子的納什適應度值越來越大,約90代后收斂于2.0,策略組合收斂至(1.3367; 1.2525),這和非線性互補算法求解的結果也完全相符。

圖6 Lmax=25 MW下進化過程中最優粒子位置及適應度

Fig. 6 Optimal particle position and fitness in evolution underLmax=25 MW

對比供給函數均衡和完全競爭下的出清結果(如表2所示),發電商在供給函數均衡下的收益普遍高于完全競爭下的,但社會福利卻低于完全競爭下的。此結果表明,在不完全競爭的市場中,發電商可以采取策略性報價增加自身收益,但以社會福利的損失為代價。再比較有阻塞和無阻塞下發電商均衡策略組合,有阻塞下發電商的均衡報價系數均高于無阻塞下,說明在阻塞情況下發電商可以在小范圍內行使市場力。同時阻塞的存在也改變了用戶的收益格局,阻塞的存在不一定會使所有發電商的收益減少,可能使某些發電商收益減少,卻使其它發電商收益增加。因線路1-2阻塞的存在,使得成本占絕對優勢的G1無法向D2供應更多的電量,D2只得轉而向成本較高的G2購電,造成了發電商中標電量顛覆性的改變,從而G2收益較無阻塞顯著增加、G1收益較無阻塞顯著減少。

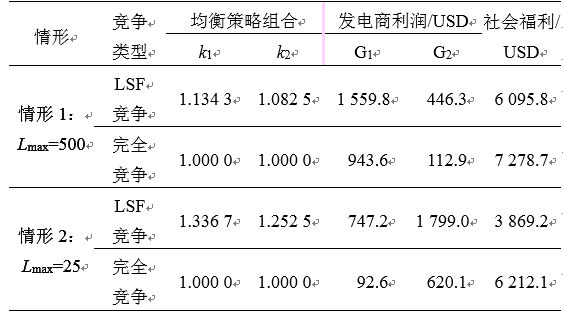
表2 不同情形下的均衡策略組合和收益情況

Tab. 2 Equilibrium strategy portfolio and income under two different conditions

4.2 IEEE 30節點測試系統

IEEE 30節點系統包含6個發電商,20個負荷,41條支路。其中,發電商成本參數如表3所示,網絡拓撲及負荷數據見附錄。選取3條潮流最大的支路1-2、12-13、15-23,設置輸電上限15 MW,使其發生阻塞。

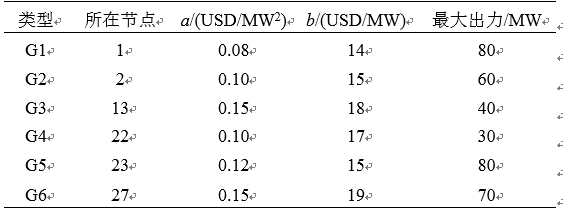
表3 發電商的參數

Tab. 3 Data of GenCo

考慮2種情況：一種為發電商間無合謀,6個發電商獨立競價;另一種為發電商間有合謀,G1/ G2/G3屬于合謀集團1,G4/G5/G6屬于合謀集團2。

仿真參數設置：外層粒子群粒子數目16,最大進化代數300;內層粒子群粒子數目10,最大進化代數200;kmin、kmax分別取1和3。

1)情形3,發電商間無合謀(6機獨立競價)。

圖7記錄了雙層粒子群算法尋優過程中最優粒子的策略組合和納什適應度值。

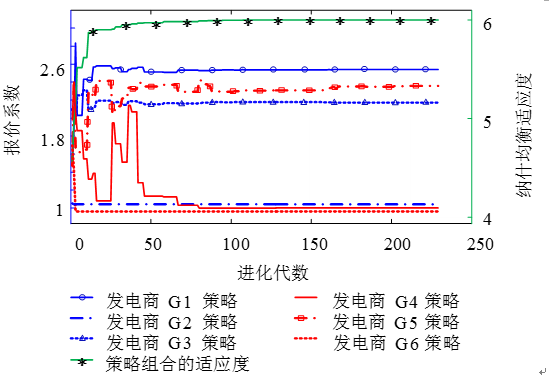
圖7 情形3(進化過程中最優粒子位置和適應度)

Fig. 7 Optimal particle position and fitness in evolution under situation 3

無合謀的情形下,收斂的均衡策略組合如表4所示,可以看到,只有發電商G1/3/5以高于邊際成本報價,而發電商G2/4/6卻按邊際成本報價。這種現象可以從出清結果中解釋：比較發電商所在節點電價和發電商邊際電價,當發電商未滿出力時,其節點電價與邊際電價是一致的,此時發電商可以通過策略性報價改變節點電價和中標量,從而改變利潤;而當發電商滿出力時,其節點電價是大于邊際電價的,此時發電商所在節點電價不再受自身策略性報價的控制,而是由未滿出力發電商的邊際電

表4 不同情形下的均衡策略組合和收益情況

Tab. 4 Equilibrium strategy portfolio and income under two different conditions

價、網絡阻塞情況決定。發電商G2/4/6的額定容量小、負荷需求量大,導致其在邊際成本一定范圍內報價均會滿出力中標,此時發電商的節點電價和中標量不受自身報價的影響,發電商報高價與報低價沒有區別,反而報價過高會導致中標量減小、利潤降低。

2)情形4,發電商間有合謀(G1/G2/G3屬于合謀集團1,G4/G5/G6屬于合謀集團2)。

在發電商間有合謀的情況下,進化過程中最優粒子的位置變化及納什適應度值如圖8所示,收斂的均衡策略組合如表4所示。

比較情形3和完全競爭下發電商的收益,如表4所示。發電商G2均按邊際成本報價,但寡頭競爭下的收益卻小于完全競爭下的。原因在與雖然兩種情況下G2的中標量都是一樣的,但由于阻塞程度不同造成寡頭競爭下節點電價低于完全競爭下的,所以G2在寡頭競爭下的利潤更低些。在完全競爭下,各發電商均按邊際成本報價,價格低了市場成交量就很大,導致線路1-2阻塞嚴重,處于阻塞線路受端的節點G2,其節點電價相比正常水平高出了許多(14行3列)。而在寡頭競爭下,部分發電商以高于邊際成本報價,價格高了市場成交量

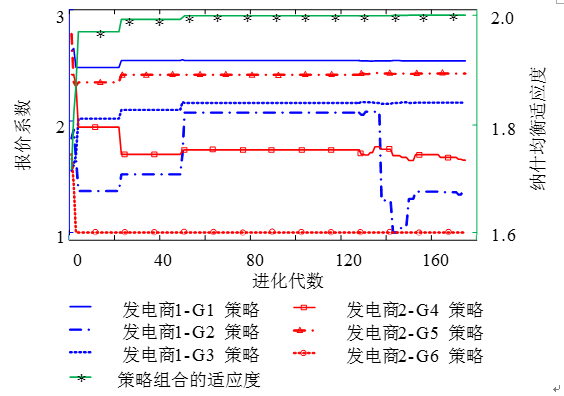
圖8 情形4(進化過程中最優粒子位置和適應度)

Fig. 8 Optimal particle position and fitness in evolution under situation 4

相對少,阻塞情況相對完全競爭減輕了,處于支路受端G2的節點電價也就相對小了一些(13行3列)。由于網絡阻塞程度不同造成的節點電價不同,引起了發電商G2在寡頭競爭時利潤比完全競爭時低。

再比較無合謀與有合謀(情形3和情形4)下發電商的均衡策略組合,有合謀下各發電商的收益未必都大于無合謀下的收益,但合謀整體的利潤均高于無合謀下的。例如：G1/G2/G3組成的合謀集團1,合謀后的總收益比無合謀高出1.6 USD;G4/G5/G6組成的合謀集團2,合謀后的總收益比無合謀高出21.3 USD,但合謀下的社會福利卻相比無合謀減少了802.9 USD。此結果表明,在不完全競爭市場中,發電商之間可以通過合謀形式彼此之間聯合報價以提升整體的利潤,卻以犧牲社會福利為代價。對此,電力監管部門應制定嚴格的電力法規和激勵措施,引導發電商披露真實邊際成本,遏制發電商間合謀競價的投機行為,促使電力市場向開放健康的方向發展。

5 結論

針對求解電力市場策略均衡的復雜問題,在綜述現有求解方法的基礎上,本文提出了雙層粒子群算法求解均衡策略,并采用標準3節點系統和IEEE 30節點系統對上述算法進行了驗證,得出了以下結論：

1)本文提出的雙層粒子群算法可以有效的用于求解電力市場均衡的問題,甚至可以延伸至求解主輔聯合市場均衡的問題。

2)發電商在寡頭競爭下的利潤不一定都比完全競爭下的高,發電商所處地理位置和自身機組的容量限制,可能導致發電商在寡頭競爭下的收益低于完全競爭下的。

3)在不完全競爭的電力市場中,發電商之間可以通過合謀提升整體利潤、削減社會福利。對此,電力監管部門應制定嚴格的電力法規,遏制發電商間合謀競價的投機行為。