作為未來重要的電力用戶,商業園區建設將成為智能電網建設的重要內容之一。商業園區中儲能系統最基本的作用是進行負荷側的削峰填谷,在給園區帶來經濟收益的同時,也保證了電網運行的安全性。提出了一種儲能系統削峰填谷的變參數功率差控制策略,基于園區典型日負荷預測曲線,對負荷狀態和儲能SOC狀態進行區間劃分,提出了對應的子目標函數,采用適應度函數變差系數排序法確定各子目標函數權重,對目標函數進行尋優,確定不同負荷區間與SOC區間的儲能系統控制策略。最后,以上海某商業園區為例進行了仿真,驗證了所提控制策略的有效性。

0 引言

近年來,隨著經濟水平的快速發展,電力系統負荷呈現出峰谷差日益增大的特點,這會降低電力系統的經濟性,并造成社會資源浪費[1],而這種現象在商業園區尤為嚴重。在商業園區中加入儲能系統,利用儲能電池蓄能特性可實現削峰填谷。儲能通過自身的充放電特性,能夠延緩園區電網的容量升級改造,提高設備利用率和供電可靠性[2-3];同時,在部分實行峰谷電價地區,用戶可通過儲能系統減小負荷峰谷差而受益。因此,儲能系統的使用在給電網安全運行帶來保障的同時,也給用戶側帶來經濟收益。

目前,關于求解儲能系統削峰填谷策略的算法主要包括動態規劃算法、智能算法等。文獻[3]針對采用恒功率充放電策略運行的電池儲能系統,結合序列二次算法提出了恒功率充放電優化模型。文

獻[4]提出了基于動態規劃的削峰填谷控制策略,同時考慮了充放電深度對電池壽命的影響,但其限制了每日的充放電次數,部分場景下由于負荷變化較大,儲能系統可能需要多次變化充放電狀態。文獻[5-7]采用智能算法求解含儲能裝置的最優策略問題,但均未考慮SOC的狀態。文獻[8]比較了儲能系統恒功率控制方式與功率差控制方式的控制效果,結果表明：與功率差控制方式相比,恒功率控制較簡單,但其控制效果不如功率差的控制方式,并且恒功率控制對負荷預測精度要求較高。還有學者在進行儲能相關研究時提出了關于SOC的狀態區間劃分。文獻[9]中將SOC按大小劃分為5個區間,判斷SOC當前工作區間,實時調整濾波常數,建立了儲能系統的容量優化配置方法。

本文針對商業園區儲能系統,提出一種協調考慮削峰填谷效果和SOC狀態區間的變參數功率差控制策略。基于商業園區典型日負荷預測曲線,將負荷劃分為3個區間,引入2個SOC狀態控制變量,將SOC劃分為5個區間,引入4個充放電功率控制變量,為每個子空間制定控制策略,并基于目標函數對變量進行滾動更新。

1 商業園區儲能系統削峰填谷的常參數功率差控制策略

1.1 商業園區電力系統構成

商業園區電力系統一般由外部電網、分布式電源、儲能系統以及冷熱電負荷(包括空調負荷、樓宇負荷等,以下統稱為負荷)組成,如圖1所示。

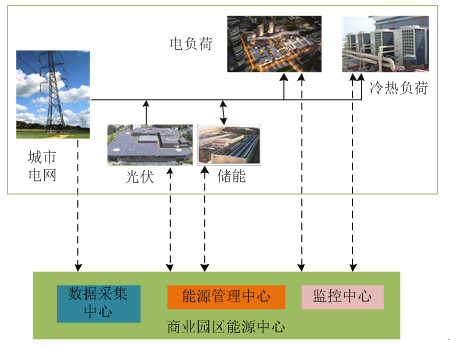
圖1 典型商業園區電力系統構成

如圖1所示,實線代表能量流流動,虛線代表信息流流動,箭頭所示方向為能量及信息流動方向。

能量在城市電網、分布式光伏陣列、儲能系統以及負荷之間流動,實現了能源生產與消費間的互

動[10]。商業園區往往在建筑屋頂配備一定規模的分布式光伏陣列,用以滿足部分負荷需求,但規模相較園區負荷較小。考慮光伏不確定性對電網的沖擊,為鼓勵光伏發電就地消納,光伏陣列優先為負荷側供電,剩余電量進行上網[11]。考慮用電持續性及光伏陣列規模有限,引入城市電網以滿足商業園區負荷需求。儲能系統的加入能夠對負荷的峰谷進行調節,從而給商業園區用戶帶來一定的經濟收益[12,13]。

商業園區能源中心主要實現對商業園區電力系統各部分的信息采集與監控管理。本文將重點考慮能源中心中儲能系統的控制策略,以實現儲能系統的高效運行。

1.2 常參數功率差控制策略

恒功率控制是儲能系統最簡單的充放電控制策略,即在任一時刻儲能系統均以恒定功率進行充放電,該策略根據典型日負荷預測曲線提前制定儲能充放電計劃,但該控制策略對典型日負荷曲線的預測精度要求較高。而功率差控制則對典型日負荷曲線預測精度要求不高,同時,功率差控制考慮了儲能電池的容量約束、出力約束等。

常參數功率差控制策略根據日負荷預測曲線,計算得出儲能系統參與充電的上限功率與放電的下限功率。具體計算流程[8,14]如圖2所示。

圖2 常參數功率差控制策略流程

圖2中, Ec為總充電量; Ed為總放電量;ε為某一接近0的常數; E為儲能系統容量;Δt為單位時間,本文選取為數據采樣分辨率。經以上步驟計算,可確定儲能系統放電時負荷的下限功率P1與儲能系統充電時負荷的上限功率P2。通過確定儲能系統充放電時的負荷上下限值,能夠將負荷狀態劃分為3個區間,如圖3所示。

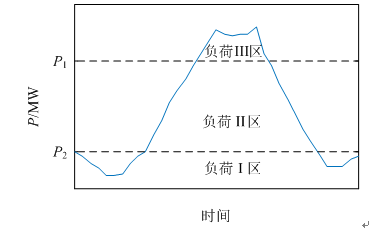
圖3 負荷區間劃分

1)儲能充電區間(負荷I區)：此區間滿足Pt≤P2Pt≤P2,其中Pt為t時刻的負荷功率。在此區間,儲能系統充電以增大負荷谷值,充電功率為

Pc=P2−Pt (1)

2)儲能靜置區間(負荷II區)：此區間滿足P2

Pc=Pd=0 (2)

3)儲能放電區間(負荷III區)：此區間滿足Pt≥P1Pt≥P1,此時儲能系統放電以減小負荷峰值,放電功率為

Pd=Pt−P1 (3)

常參數功率差控制策略通過負荷值確定儲能系統的充放電狀態以及出力大小,但該控制策略并未考慮SOC狀態。當負荷曲線峰谷持續時間較長時,儲能系統長時間充放電會對SOC值產生影響,造成SOC越限,這會對儲能系統的壽命造成影響。

2 變參數功率差控制策略

基于常參數功率差控制策略,在滿足系統功率平衡的基礎上,本文充分考慮SOC狀態,提出考慮SOC狀態的變參數功率差控制策略,使儲能系統盡可能避免出現在SOC過高/低區間,以延長其壽命。

2.1 SOC狀態區間劃分

通過引入Sup、Sdown兩個變量,將SOC狀態區間進行劃分,圖4中將SOC劃分為5個狀態區間,分別如下：

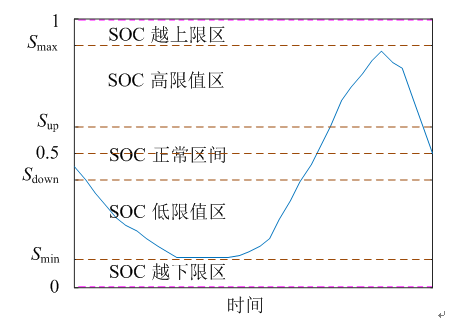
圖4 SOC狀態區間劃分

1)SOC越上限區。

Smax ≤ S(t) < 1

2)SOC高限值區。

Sup ≤ S(t) < Smax

3)SOC正常工作區。

Sdown ≤ S(t) < Sup

4)SOC低限值區。

Smin ≤ S(t) < Sdown

5)SOC越下限區。

0 < S(t) < Smin

式中：S(t)為t時刻的SOC值;Smax、Smin為儲能系統所允許的SOC的最大值與最小值;Sup、Sdown是控制SOC狀態劃分的參數,且滿足下式約束

0 < Smin < Sdown < Sup < Smax < 1 (4)

2.2 變參數功率差控制原則

變參數功率差控制策略的原則之一是通過調節SOC高低限值區的充放電功率,盡量避免或縮短SOC處于越上下限區。為此,結合所劃分的SOC狀態區間,引入控制參數k1、k2、k3、k4,其控制原則如下：

1)SOC越上限區：此區間儲能不進行充電操作。

在負荷I區,儲能系統靜置,由電網及光伏對園區負荷進行供電。

在負荷II區及III區,儲能系統放電,且以充電上限值為目標放電,考慮儲能系統功率約束,故放電功率：Pd=min(Pe,Pt−P2)Pd=min(Pe,Pt−P2);其中,Pe為儲能系統額定功率;Pt為負荷功率。

2)SOC高限值區：此區間根據所處負荷區間不同,儲能系統進行不同充放電操作。

在負荷I區,儲能系統進行充電,但由于該區間內SOC值已經較大,過大的充電功率會使SOC進入越上限區,此區間內充電功率為

Pc=k1(P2−Pt)Pc=k1(P2−Pt) (5)

其中0 < k1 <1，這樣能夠使其在負荷I區進行填谷的同時,兼顧SOC的狀態。

在負荷II區,儲能系統靜置。

在負荷III區,儲能系統進行放電操作,由于此刻的SOC值較高,很容易進入越上限區,需盡可能增大放電功率,同時放電還應受到功率約束與負荷區間約束,故此時的放電功率為

在負荷II區,儲能系統靜置。

在負荷III區,儲能系統放電,放電功率為

Pd=k4(Pt−P1)Pd=k4(Pt−P1) (10)

其中0 < k4 <1，

5)SOC越下限區：與SOC越上限區相反。

在負荷I區及II區,儲能系統充電功率為

Pc=min(Pe,P1−Pt)(11)

在負荷III區,儲能系統靜置。

將上述控制策略整理如下表1所示,其中儲能系統功率放電為正,充電為負。

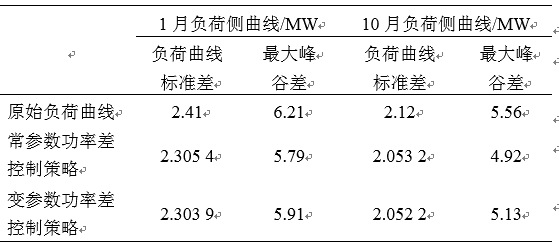
表1 變參數功率差控制策略

如表1所示,通過Sup、Sdown兩個參數變量能夠對荷電狀態區間進行劃分,通過控制參數k1、k2、k3、k4對每個區間充放電功率進行控制。協調考慮SOC狀態與負荷區間,共生成了15個充放電區間,每個區間對應不同的充放電規則。通過對Sup、Sdown、k1、k2、k3、k4等6個變量進行滾動優化,可實現協調考慮SOC狀態的變參數功率差控制策略。

2.3 變參數功率差控制策略的參數優化

考慮到負荷有一定波動性,基于典型日負荷預測曲線,考慮控制策略在未來30 min內的控制效果,對這6個控制變量的滾動更新,從而使控制策略有一定前瞻性和全局性。因此,本文的控制目標將協調未來30 min內的負荷側削峰填谷效果與SOC狀態。

2.3.1 目標函數

為對本控制策略作用下的負荷側削峰填谷效果、SOC變化情況進行評價,并鼓勵光伏發電的就地消納,提高供電滿意度,定義以下子目標函數。

1)負荷側評價指標。

為對負荷側削峰填谷效果進行評價,本文定義目標函數F1為

4)目標函數權值確定。

綜上,本控制策略的目標函數由F1,F2,F3,F4聯合構成,即

minF=min{F1,F2,F3,F4} (17)

由于F1,F2,F3,F4分別代表目標函數的不同特征,對以上4個目標函數賦予一組權重系數λi (i=1,2,3,4),即

minF=λ1F1+λ2F2+λ3F3+λ4F4 (18)

為確定各子目標函數的權重λi,本文采用適應度函數變差系數排序法。具體步驟如下。

1)設有n個子目標函數,分別計算出各子目標函數的最優解min Fi(x),記為Xi (i=1,2,…,n)。

2)對各子目標函數的最優解進行交互迭代,分別計算出對應的目標函數值Fj(xi)。

3)計算各子目標函數的不同解下的變差系數。

5)對上述權系數進行大小排序,變差系數大的目標函數乘以較小的權值,變差系數小的目標函數乘以較大的權值,以更好地均衡有效解的范圍。

2.3.2 約束條件

本文所提出的控制策略主要考慮了電網功率平衡約束、儲能系統自身約束(包括荷電狀態、充放電功率、容量)、對Sup、Sdown、k1、k2、k3、k4等6個控制參數的約束以及光伏功率倒送約束。

1)電網功率平衡約束。

為保證園區內用電設備的正常工作,需滿足電網的功率平衡,即

Pgrid+PPV=Pload−Pess (21)

其中：PgridPgrid為城市電網對園區的輸出功率;PPVPPV為園區分布式光伏陣列輸出功率;PloadPload為園區負荷功率;PessPess為儲能系統出力。

2)儲能系統自身約束。

儲能系統自身約束見式[15]

Smin≤S(t)≤Smax (22)

0≤Pc≤Pe (23)

0≤Pd≤Pe (24)

其中：Smin一般取20%~30%;Smax一般取80%~100%;Pc、Pd分別為儲能系統充放電功率;Pe為儲能系統額定功率。本控制策略考慮了SOC在兩種極端區間的控制策略,這是由于儲能系統初始SOC可能存在越限情況。

儲能系統SOC、容量與充放電功率之間還應滿足如下關系[16]。

2.3.3 動態自適應粒子群算法

基于以上目標函數和約束條件,本文采用動態自適應粒子群算法對所引入Sup、Sdown、k1、k2、k3、k4等6個參數進行滾動尋優。

粒子群算法(PSO)是一種隨機搜索、并行的優化算法,具有收斂速度快、簡單易行等優點[17]。粒子群優化算法通過群體中個體之間的協作和信息共享來尋找最優解。PSO中,粒子按下式進行位置與速度更新。

然而,由于快速的收斂算法,使得粒子群算法易早熟,從而陷入局部最優中。粒子群算法中較大的慣性權因子有利于全局探索,但會使算法收斂速度降低;而較小的慣性權因子有利于算法的局部開發,加速算法的收斂,但會使算法的全局性變差。動態自適應粒子群算法考慮了慣性權因子w對算法的影響,對慣性權因子進行動態自適應調整,令

1)設置粒子個數,迭代次數以及加速因子,并對粒子位置與速度進行初始化,使粒子初始位置位于限制范圍內。

2)根據目標函數,計算每個個體的適應度進行評價,并對個體最優解與全局最優解進行保存。

3)初次更新粒子位置與速度。

4)計算位置和速度更新后的適應度值。

5)進行迭代運算,通過首次的個體最優解

與全局最優解對慣性權因子進行更新。之后帶入

式(33)和(34),更新粒子位置與速度。

6)判斷迭代結果是否滿足終止條件,若滿足,結束迭代并輸出結果。否則返回步驟5,再次進行迭代運算。

本文采用變參數功率差控制策略,其流程圖如圖5所示。

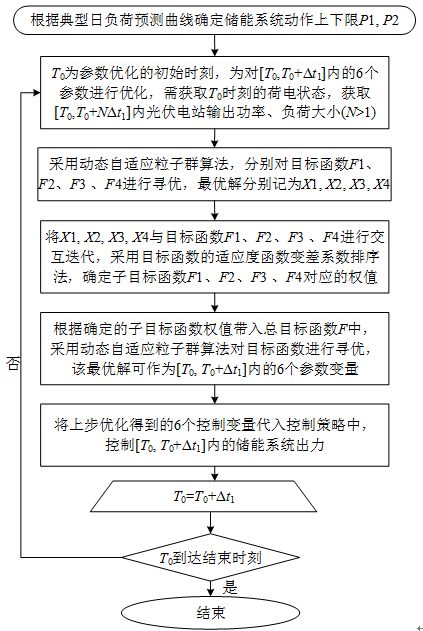
圖5 變參數功率差控制策略流程

3 算例分析

本文以上海某商業園區為例,對本控制策略的有效性進行分析。仿真所用日負荷預測曲線基于支持向量機算法得出[18],同時基于商業園區工作日的日負荷曲線整體相似的特點[19],得到了該商業園區的1月和10月工作日典型超短期日負荷預測曲線。

3.1 變參數功率差控制策略仿真

該商業園區源、儲、荷各部分配置如下：光伏系統裝機容量為3 MW;儲能系統為鋰電池,額定功率為1 MW,額定容量為2 MW?h;1月最大負荷6.5 MW,10月最大負荷5.8 MW。該商業園區1月和10月的工作日典型日負荷預測曲線及該月內某日的光伏出力曲線如圖6所示。

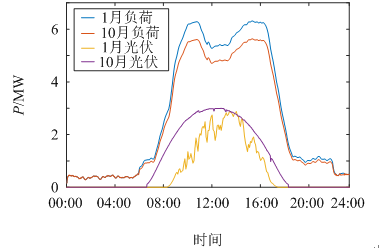
圖6 商業園區1月和10月工作日典型日負荷預測曲線及光伏出力曲線

由圖6可發現,10月負荷較1月負荷出現下降,但商業園區工作日的日負荷預測曲線形狀相似,這與工作日的負荷曲線相似有很大關系。商業園區負荷有兩個用電高峰時段,分別在上午10:30左右與下午14:30左右達到用電峰值,且峰值均會持續2~3h左右。11:30—13:00,負荷會出現短時的下降,在晚上22:00至凌晨5:00左右,負荷出現低谷。

基于該典型日負荷預測曲線,按照本控制策略的計算流程,分別計算得出：1月典型日負荷預測曲線均值Pavg=2.58 MW,放電下限P1=5.96 MW,充電上限P2=0.52 MW;10月典型日負荷預測曲線均值Pavg=2.40 MW,放電下限P1=5.21 MW,充電上限P2=0.50 MW。

基于圖6中1月與10月負荷數據進行仿真,考慮采樣數據的分辨率,每隔10 min對Sup、Sdown、k1、k2、k3、k4等6個參數進行更新一次。基于負荷預測曲線,以未來30 min的目標函數最優作為本區間的最優解,這樣使本控制策略有了預見性和一定的全局性。

設置動態自適應粒子群算法粒子數n=50,最大迭代次數k=300,加速因子c1=c2=1.5;SOC上下

限Smin=0.2,Smax=0.8,儲能系統自放電率為0,充放電效率均為100%,設定最大光伏倒送功率

約束為1 MW。依圖5流程進行仿真,仿真結果如圖7—9所示。

圖7 變參數功率差控制策略作用下的SOC曲線

圖7中可看出儲能系統的SOC在整個周期內均保持在的上下邊限[0.2,0.8]之間,實現了SOC變化范圍的有效控制。這是因為本文方法引入6個參數變量,通過優化6個參數變量,而優化儲能系統SOC區間與充放電功率,同時考慮未來30 min內的控制效果,實現對當前10 min內6個變量的滾動更新。考慮到當前儲能系統成本仍然較高,而保持SOC在較優的變化范圍內有利于延長儲能系統的壽命,有效降低儲能系統的運行成本。因此,本控制策略將有利于降低儲能系統的工程成本。

圖8 變參數功率差控制策略作用下1月荷側功率曲線

圖9 變參數功率差控制策略作用下10月負荷側功率曲線

由圖8及圖9可見,該控制策略下,儲能系統確實起到了削峰填谷的作用,儲能系統在22:00—6:00間進行充電操作,增大了原始負荷曲線的谷段負荷;儲能系統在9:00—12:00,13:00—15:00進行放電操作,減小了原始負荷曲線峰段負荷。本文提出的策略達到了兼顧儲能SOC性能指標和削峰填谷的綜合優化效果。

3.2 與常參數功率差控制效果對比

為了進一步驗證本文提出策略的控制效果,將本文提出的基于綜合目標函數粒子群優化的變參數功率差控制策略與常參數功率差控制策略進行了仿真對比,如圖10—13所示。

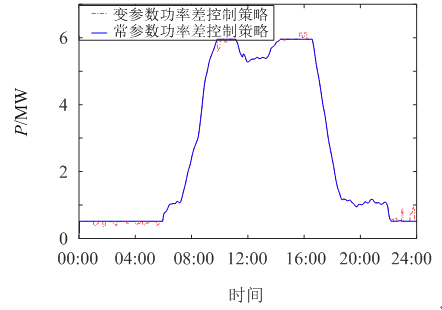
圖10 不同控制策略作用下1月負荷側功率曲線

圖11 不同控制策略作用下10月負荷側功率曲線

圖12 1月不同控制策略作用下SOC曲線

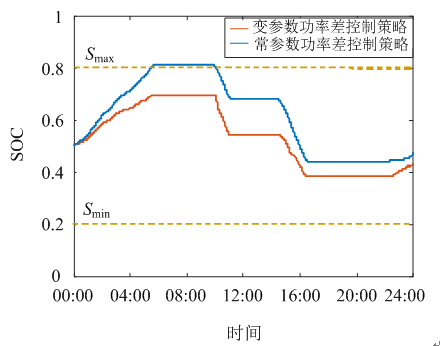
圖13 10月不同控制策略作用下SOC曲線

為對兩種控制策略進行評價,以負荷曲線標準差和峰谷差作為削峰填谷評價指標,得到不同控制策略下的結果如表2所示。

表2 不同控制策略作用下削峰填谷效果對比

由表2可見,相較原始負荷曲線,兩種控制策略都能夠有效減小負荷曲線的峰谷差和提高負荷側曲線的平滑度,起到了削峰填谷作用。相較常參數功率差控制策略,變參數功率差控制策略作用下的負荷曲線標準差更小。在最大峰谷差指標上,變參數功率差控制策略稍微有所增大,這是由于其對SOC的協調考慮,在保證較優的儲能電池SOC時,使得負荷曲線會出現短時的凹凸點,因此也稍微加大了負荷的峰谷差。

圖12—13是兩種方法SOC的曲線變化情況。從圖中可以看出常參數功率差控制策略作用下會使電池SOC出現越上限情況(SOC最大值超過0.8),這會對儲能系統壽命造成較大影響。而本算法的控制策略是在保證削峰填谷的同時兼顧使電池具備較優的SOC運行狀態,可有效減小SOC變化范圍。以圖12中1月仿真曲線為例,常參數控制策略下其變化區間為[0.4412,0.8168],變化大小為0.3756;變參數控制策略作用下變化區間[0.3992, 0.7209],變化大小為0.3217,與前者相比變化區間和變化范圍都有所減小。考慮到目前儲能系統成本較高,因此,本控制策略可有效降低儲能系統配置成本。

常參數功率差控制策略出現SOC值大于0.8情況的原因可分析如下：從圖6的原始負荷曲線中可以發現,商業園區的原始負荷曲線存在峰谷區持續時間較長的特點,而常參數功率差控制策略在確定儲能動作邊界值之后,以負荷與邊界值P1、P2的功率差進行充放電,園區負荷谷值區最初在凌晨00:00—06:00出現,由于長時間以最大功率差進行充電而使SOC進入越上限區。這種SOC指標進入越上限區的過充行為,會縮短儲能電池的使用壽命,從而間接增加儲能系統的工程運行成本,因此常參數功率差控制策略是以犧牲電池的壽命為代價換取較小的峰谷差和削峰填谷效果。

考慮到常系數功率差控制進行充放電功率調節時所依據的僅僅是邊界值P1、P2,并未考慮SOC狀態,無法根據SOC狀態調節儲能系統自身充放電功率,因此本文提出了綜合考慮削峰填谷和電池SOC狀態的變參數功率調節策略。具有以下優點：在起到削峰填谷作用(見表2)的同時,還能夠有效調節SOC變化,將SOC一直控制在合理范圍內,這對儲能電池優化運行和延長電池使用壽命具有重要意義,有很大的工程應用價值。本文所提出的方法通過引入并動態更新Sup、Sdown、k1、k2、k3、k4等6個參數,使得其能夠有效預見SOC變化,并根據SOC的狀態調節儲能系統出力,實現對SOC的自適應調節。該控制策略中,在保證削峰填谷的同時,整個過程都能夠有效將SOC控制在[0.3, 0.75]之內(見圖12—13),真正達到了同時兼顧削峰填谷作用和優化電池SOC運行狀態的雙重效果。

以基于1月份典型負荷預測曲線為例,仿真中對應的Sup、Sdown、k1、k2、k3、k4等6個參數及各子目標函數權重λi (i=1,2,3,4)的變化情況如圖14、圖15、圖16所示。

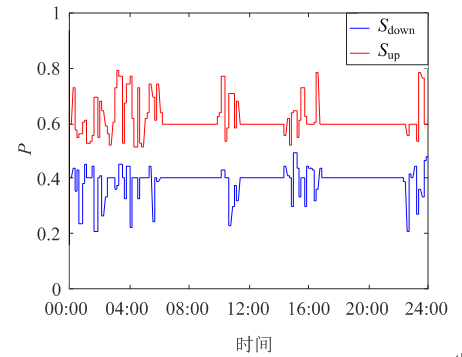
圖14 Sup與Sdown變化曲線

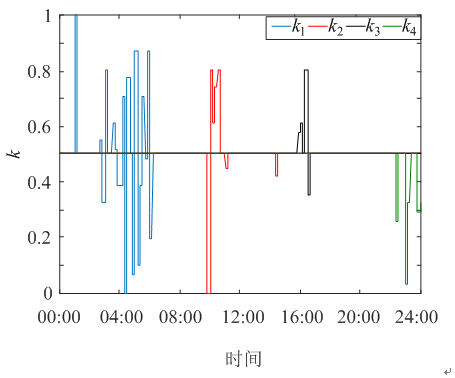
圖15 k1、k2、k3、k4變化曲線

圖16 λ1、λ2、λ3、λ4變化曲線

在上午00:00—6:00,兩種控制策略作用下,儲能系統均進行了充電操作;其中00:00—02:00左右,SOC一直處于正常工作區,與此同時,Sup與Sdown兩參數一直處于動態更新之中,此時段內兩條SOC曲線重合。在02:00左右開始,儲能系統SOC達到0.6左右,而Sup也更新至0.6左右,進入SOC越上

限區,k1動作,有效減小了儲能系統出力。表現在圖8中則是負荷側曲線在00:00—06:00間會有凹點。同理可見k2、k3、k4出力時刻,對應負荷側曲線均會間歇性出現小的凹凸點。由于本控制策略預估了未來30 min內SOC的狀態,故而k1、k2、k3、k4的變化有一定的波動性。Sup、Sdown又與當前時刻k1、k2、k3、k4相關,因此,這兩組參數相互協調。變系數控制策略由于SOC區間限制,會在SOC高限值區間內降低充電速率,SOC曲線上升速率較常參數控制策略作用下的SOC曲線上升速率變慢。在上午9:00—12:00,出現負荷高峰,由于此時SOC均處于高限值區,k2動作,有效增大了放電功率,表現在該段區間內初始一段時間內的SOC曲線下降速率大于常系數控制策略下的SOC曲線,而Sup也隨之滾動更新,11:00左右,SOC從高限值區進入正常工作區,兩種控制策略下的曲線下降速率相同。同理,13:00—16:00及22:00—24:00區間內的SOC曲線速率也會不同,但由于此時經過一次放電或者第二次放電一段時間之后,SOC進入低限值區,故而此時出現與之前時刻相反的情形。由圖16中可見,子目標函數λ1與λ2所占權重在各時段內均明顯高λ3與λ4因此,目標函數對于負荷側曲線的波動性和SOC防止越限賦予了較大的權重,這與本控制策略中著重考慮了SOC變化特性和負荷側平滑度有關,這與仿真中SOC曲線有較明顯下降的分析結果相一致。

3.3 與基于實際負荷曲線的控制效果對比

目前,針對儲能系統參與削峰填谷的控制策略大多是基于實際負荷曲線進行的,而本控制策略中采用了基于支持向量機算法得到的超短期負荷預測曲線,負荷預測曲線的引入主要為使本控制策略具有一定的全局性和前瞻性。本節中將通過對比基于預測負荷曲線和實際負荷曲線的控制策略作用效果,以上海商業園區1月某工作日實際負荷曲線與工作日典型負荷預測曲線進行仿真,從而論證了引入負荷預測曲線的優越性。基于典型負荷預測曲線下該控制策略能夠通過協調考慮未來30 min內的控制效果,對比不考慮負荷預測情況下,基于實際負荷曲線僅考慮當下時刻的控制效果,圖17給出了兩種情況下的控制效果對比。

圖17 控制效果對比

由上圖看見,引入負荷預測曲線能夠明顯降低負荷側峰谷差,而實際負荷曲線下,由于未考慮下一時刻的控制效果,目標函數僅以當前整10 min內的SOC狀態和負荷側波動性為主進行調節,因此,減少了儲能的出力,其控制效果有所降低。

4 結論

本文提出了一種商業園區儲能系統的變參數功率差控制策略,主要內容包括：

1)基于商業園區典型日負荷預測曲線,確定儲能系統動作上下限,將負荷劃分為3個區間。引入2個SOC狀態控制變量,將SOC劃分為5個區間。在不同SOC狀態區間與不同負荷區間,為儲能系統制定了不同充放電策略。

2)為評估儲能削峰填谷效果與SOC狀態,引入4個子目標函數,采用適應度函數變差系數排序法確定各子目標函數權重,對加權后的目標函數采用動態自適應粒子群算法進行尋優,確定不同狀態區間和負荷區間儲能系統控制參數。

3)本控制策略是基于典型日負荷預測曲線制定的,因此,能夠統籌未來30 min內的控制效果,通過與基于實際負荷曲線的控制效果對比,驗證了其前瞻性和優越性。

4)由于控制策略中協調考慮了儲能系統SOC變化的影響,避免了儲能系統出現SOC越限情況,同時,可有效調節SOC變化范圍,考慮到目前儲能系統配置成本較高,通過有效降低SOC變化范圍能夠減小工程成本。

但由于目前對儲能削峰填谷效果評估缺乏統一標準,園區負荷預測精度仍有待提高,因此進一步研究園區負荷預測精度不同對本文控制效果的影響,將是論文后續研究內容。

(本文作者：楊錫運, 董德華, 李相俊, 馬雪, 耿娜, 賈學翠)

參考文獻

[1] 鄭雪冰. 利用儲能電池進行削峰填谷的多指標綜合評價方法[D].北京:華北電力大學,2015.

[2] 寧陽天,李相俊,麻秀范,等.考慮供電可靠性的電池儲能系統削峰填谷策略研究[J].電氣應用,2015,34(6):62-68. Ning Yangtian,Li Xiangjun,Ma Xiufan,et al.Study on peak-filling strategy of battery energy storage system considering power supply reliability[J].Electrotechnical Application,2015,34(6):62-68(in Chinese).

[3] 陳滿,陸志剛,劉怡,等.電池儲能系統恒功率削峰填谷優化策略研究[J].電網技術,2012,36(9):232-237. Chen Man,Lu Zhigang,Liu Yi,et al.Research on optimal peak load shifting strategy of battery energy storage system operated in constant power mode[J].Power System Technology,2012,36(9):232-237(in Chinese).

[4] 鮑冠南,陸超,袁志昌,等.基于動態規劃的電池儲能系統削峰填谷實時優化[J].電力系統自動化,2012,36(12):11-16. Bao Guannan,Lu Chao,YuanZhichang,et al.Load shift real-time optimization strategy of battery energy storage system based on dynamic programming[J].Automation of Electric Power Systems,2012,36(12):11-16(in Chinese).

[5] Chacra F A,Bastard P,Fleury G,et al.Impact of energy storage costs on economical performance in a distribution substation[J].IEEE Trans on Power Systems,2005,20(2):684-691.

[6] Lee T Y.Operating schedule of battery energy storage system in a time-of-use rate industrial user with wind turbine generators: a multipass iteration particle swarm optimization approach[J].IEEE Trans on Energy Conversion,2007,22(3):774-782.

[7] Cau T D H,Kaye R J.Evolutionary optimization method for multistorage hydrothermal scheduling[J].IEE Proceedings of Generation Transmission and Distribution,2002,149(2):152-156.

[8] 陳益哲,張步涵,王江虹,等.基于短期負荷預測的微網儲能系統主動控制策略[J].電網技術,2011,35(8):35-40. Chen Yizhe,Zhang Buhan,Wang Jianghong,et al.Active control strategy for microgrid energy storage system based on short-term load foreing[J].Power System Technology,2011,35(8):35-40(in Chinese).

[9] 王偉,薛金花,葉季蕾,等.基于SOC調控的用于抑制光伏波動的電池儲能優化控制方法[J].電力系統保護與控制,2014,42(2):75-80. Wang Wei,Xue Jinhua,Ye Jilei,et al.An optimization control design of battery energy storage based on SOC for leveling off the PV power fluctuation[J].Power System Protection and Control,2014,42(2):75-80(in Chinese).

[10] 王冉,王丹,賈宏杰,等.一種平抑微網聯絡線功率波動的電池及虛擬儲能協調控制策略[J].中國電機工程學報,2015,35(20):5124-5134. Wang Ran,Wang Dan,Jia Hongjie,et al.A coordination control strategy of battery and virtual energy storage to smooth the micro-grid tie-line power fluctuations[J].Proceedings of the CSEE,2015,35(20):5124-5134(in Chinese).

[11] 趙波,包侃侃,徐志成,等.考慮需求側響應的光儲并網型微電網優化配置[J].中國電機工程學報,2015,35(21):5465-5474. Zhao Bo,Bao Kankan,Xu Zhicheng,et al.Optimal sizing for grid-connected pv-and-storage microgrid considering demand response[J].Proceedings of the CSEE,2015,35(21):5465-5474(in Chinese).

[12] Li Xiangjun,Yao Liangzhong,Dong Hui.Optimal control and management of large–scale battery energy storage system to mitigate the fluctuation and intermittence of renewable generations[J].Journal of Modern Power Systems and Clean Energy,2016,4(4):593-603.

[13] Li Xiangjun,Xu Liangfei,Hua Jianfeng,et al.Power management strategy for vehicular-applied hybrid fuel cell/battery power system.Journal of Power Sources,2009,191(2):542-549.

[14] 褚衍廷,董海鷹,李曉青.含蓄電池的孤立微電網系統運行優化研究[J].鄭州大學學報(理學版),2016,48(4):109-115. Chu Yanting,Dong Haiying,Li Xiaoqing.Optimal operation of isolated microgrid system with battery storage[J].Journal of Zhengzhou University(Natural Science Edition),2016,48(4):109-115 (in Chinese).

[15] 李相俊,張晶瓊,何宇婷,等.基于自適應動態規劃的儲能系統優化控制方法[J].電網技術,2016,40(5):1355-1362. Li Xiangjun,Zhang Jingqiong,He Yuting,et al.Optimal controlmethod of energy storage system based on adaptive dynamic programming[J].Power System Technology,2016,40(5):1355-1362 (in Chinese).

[16] 佘慎思,李征,蔡旭.風儲聯合發電系統電池荷電狀態和功率偏差控制策略[J].電力系統自動化,2014,38(20):9-17. She Shensi,Li Zheng,Cai Xu.SOC and power deviation control strategy for hybrid generation system of wind power and energy storage[J].Automation of Electric Power Systems,2014,38(20):9-17 (in Chinese).

[17] 張頂學,關治洪,劉新芝.一種動態改變慣性權重的自適應粒子群算法[J].控制與決策,2008,23(11):1253-1257. Zhang Dingxue,Guan Zhihong,Liu Xinzhi.Adaptive particle swarm optimization algorithm with dynamically changing inertia weight[J].Contrlo and Decision 2008,23(11):1253-1257(in Chinese).

[18] 王奔,冷北雪,張喜海,等.支持向量機在短期負荷預測中的應用概況[J].電力系統及其自動化學報,2011,23(4):115-121. Wang Ben,Leng Beixue,Zhang Xihai,et al.Application profiles of support vector machine in short-term load foreing[J].Proceedings of the CSU-EPSA,2011,23(4):115-121(in Chinese).

[19] 沈沉,秦建,盛萬興,等.基于小波聚類的配變短期負荷預測方法研究[J].電網技術,2016,40(2):521-526. Shen Chen,Qin Jian,Sheng Wanxing,et al.Study on short-term foreing of distribution transformer load using wavelet and clustering method[J].Power System Technology,2016,40(2):521-526 (in Chinese).