聚類是一種將數(shù)據(jù)點按一定規(guī)則分群的機器學習技術。

給定一組數(shù)據(jù)點，我們可以使用聚類算法將每個數(shù)據(jù)點分類到一個特定的簇中。理論上，屬于同一類的數(shù)據(jù)點應具有相似的屬性或特征，而不同類中的數(shù)據(jù)點應具有差異很大的屬性或特征。

聚類屬于無監(jiān)督學習中的一種方法，也是一種在許多領域中用于統(tǒng)計數(shù)據(jù)分析的常用技術。在數(shù)據(jù)科學中，我們可以使用聚類分析，來獲得一些有價值的信息。其手段是在應用聚類算法時，查看數(shù)據(jù)點會落入哪些類。

現(xiàn)在，我們來看看數(shù)據(jù)科學家們需要掌握的5種常見聚類算法以及它們的優(yōu)缺點！　　▌K-均值聚類　　K-Means可能是最知名的聚類算法，沒有之一。在很多介紹性的數(shù)據(jù)科學和機器學習課程中，都有講授該算法。并且該算法的代碼很容易理解和實現(xiàn)！你可以通過看下面的插圖來理解它。

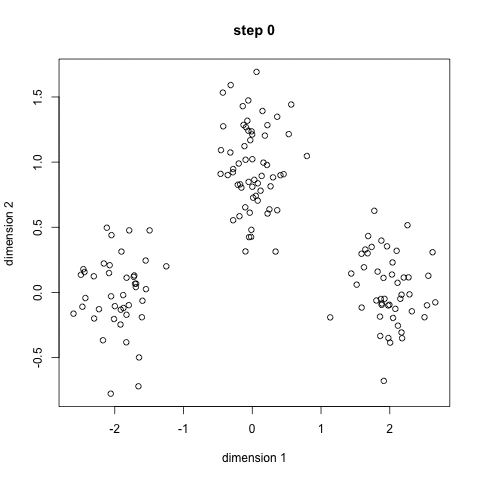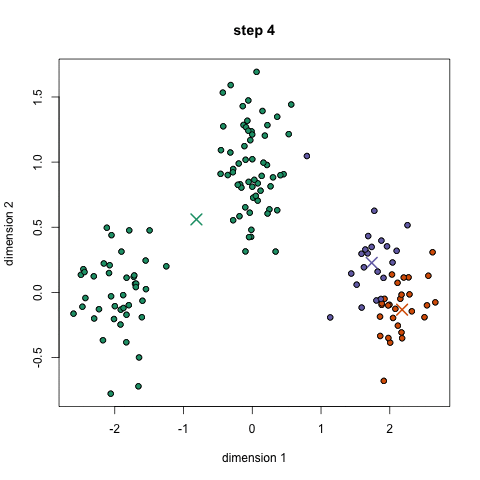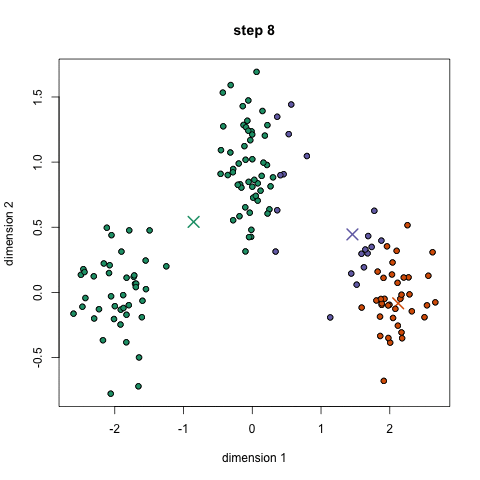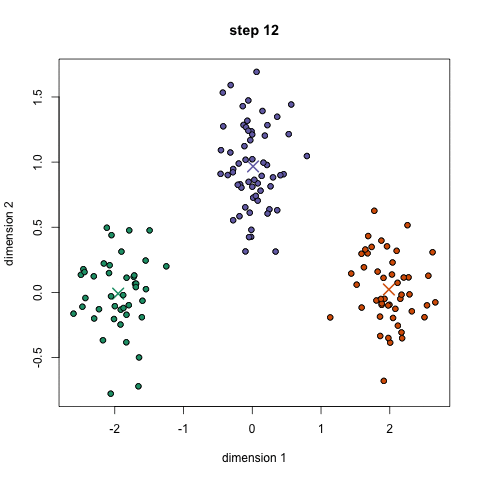
K均值聚類

1、首先，我們選擇一些要使用的類/組，并隨機初始化他們各自的中心點（質心）。要計算出簇（類）的使用數(shù)量，最好的方法是快速查看一下數(shù)據(jù)并嘗試鑒別有多少不同的分組。中心點是一個矢量，它到每個數(shù)據(jù)點的矢量長度相同，在上圖中用“X”來表示?！　?、每個數(shù)據(jù)點通過計算該點與每個簇中心之間的距離來進行分類，根據(jù)最小距離，將該點分類到對應中心點的簇中?！　?、根據(jù)這些已分類的點，我們重新計算簇中所有向量的均值，來確定新的中心點?！　?、重復以上步驟來進行一定數(shù)量的迭代，或者直到簇中心點在迭代之間變化不大。你也可以選擇多次隨機初始化簇中心點，然后選擇看起來像是最佳結果的數(shù)據(jù)，再來重復以上步驟?！　-Means算法的優(yōu)勢在于它的速度非常快，因為我們所做的只是計算點和簇中心之間的距離; 這已經(jīng)是非常少的計算了！因此它具有線性的復雜度O(n)?！　〉牵琄-Means算法也是有一些缺點。首先，你必須手動選擇有多少簇。

這是一個很大的弊端，理想情況下，我們是希望能使用一個聚類算法來幫助我們找出有多少簇，因為聚類算法的目的就是從數(shù)據(jù)中來獲得一些有用信息。

K-means算法的另一個缺點是從隨機選擇的簇中心點開始運行，這導致每一次運行該算法可能產(chǎn)生不同的聚類結果。

因此，該算法結果可能具有不可重復，缺乏一致性等性質。而其他聚類算法的結果則會顯得更一致一些。　　K-Medians是與K-Means類似的另一種聚類算法，它是通過計算類中所有向量的中值，而不是平均值，來確定簇的中心點。

這種方法的優(yōu)點是對數(shù)據(jù)中的異常值不太敏感，但是在較大的數(shù)據(jù)集時進行聚類時，速度要慢得多，造成這種現(xiàn)象的原因是這種方法每次迭代時，都需要對數(shù)據(jù)進行排序。　　▌Mean-Shift聚類算法　　Mean-Shift是一種基于滑動窗口的聚類算法。也可以說它是一種基于質心的算法，這意思是它是通過計算滑動窗口中的均值來更新中心點的候選框，以此達到找到每個簇中心點的目的。然后在剩下的處理階段中，對這些候選窗口進行濾波以消除近似或重復的窗口，找到最終的中心點及其對應的簇?？纯聪旅娴膱D解。

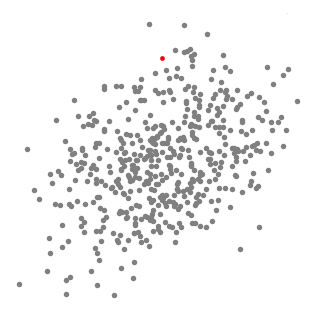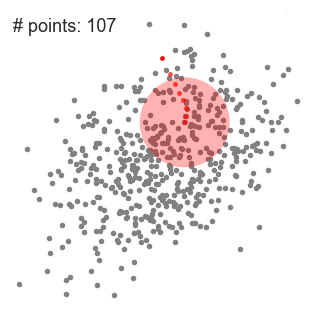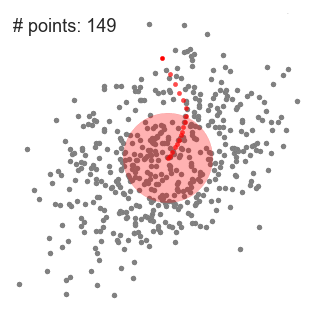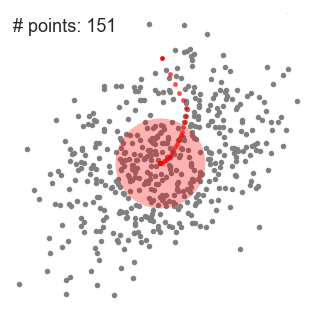
用于單個滑動窗口的Mean-Shift聚類算法

1、為了闡釋Mean-shift算法，我們可以考慮二維空間中的一組點，如上圖所示。我們從一個以C點（隨機選擇）為中心，以半徑r為核心的圓滑動窗口開始。Mean-shift可以看作是一種等高線算法，在每次迭代中，它能將核函數(shù)（圓滑動窗口）移動到每個迭代中較高密度的區(qū)域，直至收斂。　　2、在每次迭代中，通過將中心點移動到窗口內(nèi)點的平均值處（因此得名），來使滑動窗口移向更高密度的區(qū)域?；瑒哟翱趦?nèi)的數(shù)據(jù)密度與其內(nèi)部點的數(shù)目成正比。當然，通過移動窗口中點的平均值，它（滑動窗口）就會逐漸移向點密度更高的區(qū)域。　　3、我們繼續(xù)根據(jù)平均值來移動滑動窗口，直到不能找到一個移動方向，使滑動窗口可以容納更多的點。看看上面圖片的動畫效果；直到滑動窗口內(nèi)不再增加密度（即窗口中的點數(shù)），我們才停止移動這個圓圈?！　?、步驟1至步驟3的過程是由許多滑動窗口來完成的，直到所有的點都能位于對應窗口內(nèi)時才停止。當多個滑動窗口重疊時，該算法就保留包含最多點的窗口。最終所有數(shù)據(jù)點根據(jù)它們所在的滑動窗口來確定分到哪一類。　　下圖顯示了所有滑動窗口從頭到尾的整個移動過程。每個黑點代表滑動窗口的質心，每個灰點代表一個數(shù)據(jù)點。

Mean-Shift聚類的整個過程

與K-means聚類算法相比，Mean-shift算法是不需要選擇簇的數(shù)量，因為它是自動找尋有幾類。這是一個相比其他算法巨大的優(yōu)點。而且該算法的聚類效果也是非常理想的，在自然數(shù)據(jù)驅動的情況下，它能非常直觀的展現(xiàn)和符合其意義。算法的缺點是固定了窗口大小/半徑“r”。　　▌基于密度的噪聲應用空間聚類（DBSCAN）　　DBSCAN是一種基于密度的聚類算法，類似于Mean-shift算法，但具有一些顯著的優(yōu)點。我們從看下面這個奇特的圖形開始了解該算法。

DBSCAN笑臉人臉聚類

1、DBSCAN算法從一個未被訪問的任意的數(shù)據(jù)點開始。這個點的鄰域是用距離epsilon來定義（即該點ε距離范圍內(nèi)的所有點都是鄰域點）?！　?、如果在該鄰域內(nèi)有足夠數(shù)量的點（根據(jù)minPoints的值），則聚類過程開始，并且當前數(shù)據(jù)點成為新簇中的第一個點。否則，該點將被標記為噪聲（稍后，這個噪聲點可能成為聚類中的一部分）。在這兩種情況下，該點都會被標記為“已訪問”。　　3、對于新簇中的第一個點，它的ε距離鄰域內(nèi)的點也會成為同簇的一部分。這個過程使ε鄰域內(nèi)的所有點都屬于同一個簇，然后對才添加到簇中的所有新點重復上述過程?！　?、重復步驟2和3兩個過程直到確定了聚類中的所有點才停止，即訪問和標記了聚類的ε鄰域內(nèi)的所有點?！　?、一旦我們完成了當前的聚類，就檢索和處理新的未訪問的點，就能進一步發(fā)現(xiàn)新的簇或者是噪聲。重復上述過程，直到所有點被標記為已訪問才停止。由于所有點已經(jīng)被訪問完畢，每個點都被標記為屬于一個簇或是噪聲。　　與其他聚類算法相比，DBSCAN具有很多優(yōu)點。首先，它根本不需要確定簇的數(shù)量。不同于Mean-shift算法，當數(shù)據(jù)點非常不同時，會將它們單純地引入簇中，DBSCAN能將異常值識別為噪聲。另外，它能夠很好地找到任意大小和任意形狀的簇?！　BSCAN算法的主要缺點是，當數(shù)據(jù)簇密度不均勻時，它的效果不如其他算法好。這是因為當密度變化時，用于識別鄰近點的距離閾值ε和minPoints的設置將隨著簇而變化。在處理高維數(shù)據(jù)時也會出現(xiàn)這種缺點，因為難以估計距離閾值ε。　　▌使用高斯混合模型（GMM）的期望最大化（EM）聚類　　K-Means算法的主要缺點之一就是它對于聚類中心平均值的使用太單一。

通過查看下面的圖例，我們可以明白為什么它不是使用均值最佳的方式。

在左側，人眼看起來非常明顯的是，具有相同均值的數(shù)據(jù)中心點，卻是不同半徑長度的兩個圓形簇。

而K-Means算法不能解決這樣的數(shù)據(jù)問題，因為這些簇的均值是非常接近的。

K-Means算法在簇不是圓形的情況下也一樣無效，也是由于使用均值作為集群中心。

K-Means算法兩個失敗的案例

相較于K-means算法，高斯混合模型（GMMs）能處理更多的情況。對于GMM，我們假設數(shù)據(jù)點是高斯分布的; 這是一個限制較少的假設，而不是用均值來表示它們是圓形的。這樣，我們有兩個參數(shù)來描述簇的形狀：即均值和標準差！以二維為例，這意味著這些簇可以是任何類型的橢圓形（因為GMM在x和y方向上都有標準偏差）。因此，每個高斯分布都被單個簇所指定?！　榱苏业矫總€簇的高斯參數(shù)（例如平均值和標準差），我們將使用期望最大化（EM）的優(yōu)化算法。請看下面的圖表，可以作為匹配簇的高斯圖的闡釋。然后我們來完成使用GMM的期望最大化聚類過程。

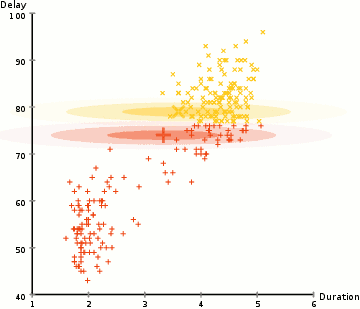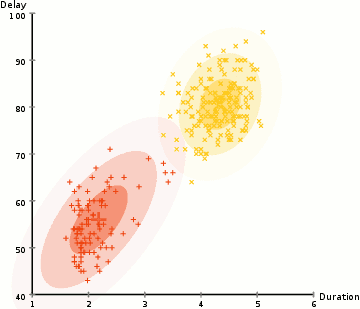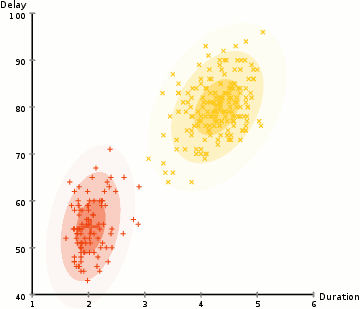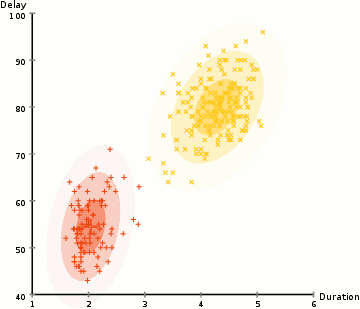
使用GMM的EM聚類

1、我們首先選擇簇的數(shù)量（如K-Means），然后隨機初始化每個簇的高斯分布參數(shù)?？梢酝ㄟ^快速查看數(shù)據(jù)的方式，來嘗試為初始參數(shù)提供一個較好的猜測。不過請注意，從上圖可以看出，這不是100％必要的，因為即使是從一個很差的高斯分布開始，算法也能很快的優(yōu)化它。　　2、給定每個簇的高斯分布，計算每個數(shù)據(jù)點屬于特定簇的概率。一個點越靠近高斯的中心，它越可能屬于該簇。在使用高斯分布時這應該是非常直觀的，因為我們假設大部分數(shù)據(jù)更靠近簇的中心?！　?、基于這些概率，我們?yōu)楦咚狗植加嬎阋唤M新的參數(shù)，使得我們能最大化簇內(nèi)數(shù)據(jù)點的概率。我們使用數(shù)據(jù)點位置的加權和來計算這些新參數(shù)，其中權重是數(shù)據(jù)點屬于該特定簇的概率。為了更直觀的解釋這個，我們可以看看上面的圖片，特別是黃色的簇。第一次迭代時，分布是隨機開始，但是我們可以看到大部分黃點都在分布的右側。當我們計算按概率加權的和時，即使中心附近的點大部分都在右邊，通過分配的均值自然就會接近這些點。我們也可以看到，大部分數(shù)據(jù)點都是“從右上到左下”。因此，改變標準差的值，可以找到一個更適合這些點的橢圓，以最大化概率加權的總和?！　?、重復迭步驟2和3，直到收斂，也就是分布在迭代中基本再無變化?！　∈褂肎MM方法有兩個很重要的優(yōu)點。 首先，GMM方法在聚類協(xié)方差上比K-Means靈活得多; 由于使用了標準偏差參數(shù)，簇可以呈現(xiàn)任何橢圓形狀，而不是被限制為圓形。 K-mean算法實際上是GMM的一個特殊情況，即每個簇的協(xié)方差在所有維度上都接近0。其次，由于GMM使用了概率，每個數(shù)據(jù)點可以有多個簇。因此，如果一個數(shù)據(jù)點位于兩個重疊的簇的中間，我們可以簡單地定義它的類，即屬于類1的概率是百分之X，屬于類2的概率是百分之Y。即，GMM支持混合類這種情況。　　▌凝聚層次聚類　　分層聚類算法實際上分為兩類：自上而下或自下而上。

自下而上的算法首先將每個數(shù)據(jù)點視為一個單一的簇，然后連續(xù)地合并（或聚合）成對的簇，直到所有的簇都合并成一個包含所有數(shù)據(jù)點的簇。

因此，自下而上的分層聚類被稱為合成聚類或HAC。

這個簇的層次可以用樹（或樹狀圖）表示。樹的根是收集所有樣本的唯一簇，葉是僅具有一個樣本的簇。

在進入算法步驟之前，請查看下面的圖解。

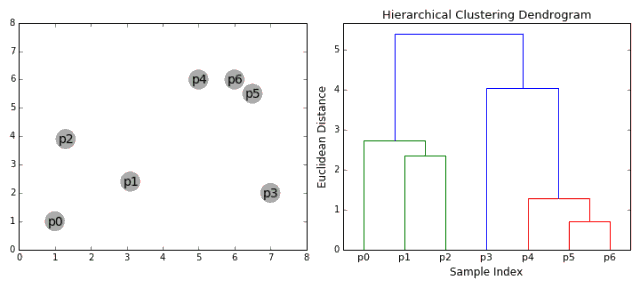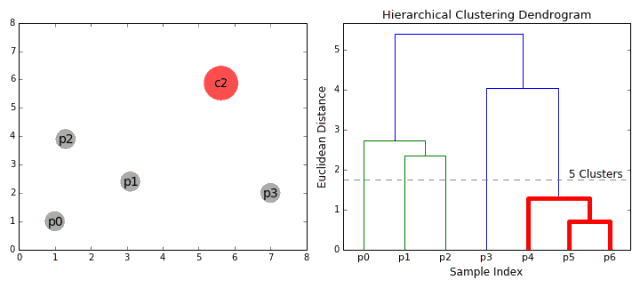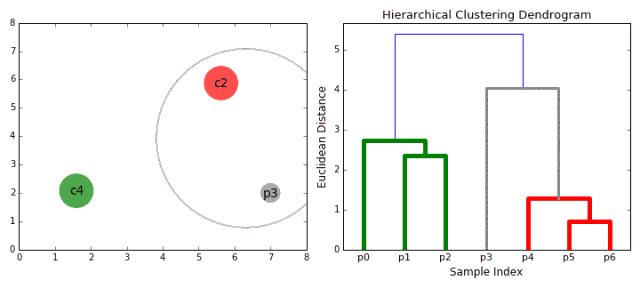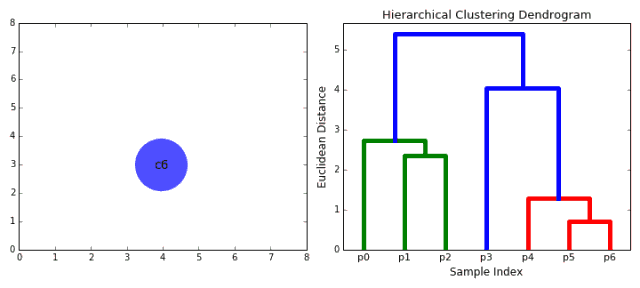
合成聚類

1、我們首先將每個數(shù)據(jù)點視為一個單一的簇，即如果我們的數(shù)據(jù)集中有X個數(shù)據(jù)點，那么我們就有X個簇。然后，我們選擇一個距離度量，來度量兩個簇之間距離。作為一個例子，我們將使用平均關聯(lián)度量，它將兩個簇之間的距離定義為第一個簇中的數(shù)據(jù)點與第二個簇中的數(shù)據(jù)點之間的平均距離?！　?、在每次迭代中，我們將兩個簇合并成一個簇。選擇平均關聯(lián)值最小的兩個簇進行合并。根據(jù)我們選擇的距離度量，這兩個簇之間的距離最小，因此是最相似的，所有應該合并。　　3、重復步驟2直到我們到達樹的根，即我們只有一個包含所有數(shù)據(jù)點的簇。通過這種方式，我們可以選擇最終需要多少個簇。方法就是選擇何時停止合并簇，即停止構建樹時！　　分層次聚類不需要我們指定簇的數(shù)量，我們甚至可以在構建樹的同時，選擇一個看起來效果最好的簇的數(shù)量。

另外，該算法對距離度量的選擇并不敏感；

與其他距離度量選擇很重要的聚類算法相比，該算法下的所有距離度量方法都表現(xiàn)得很好。

當基礎數(shù)據(jù)具有層次結構，并且想要恢復層次結構時，層次聚類算法能實現(xiàn)這一目標；

而其他聚類算法則不能做到這一點。

與K-Means和GMM的線性復雜性不同，層次聚類的這些優(yōu)點是以較低的效率為代價，即它具有O（n3）的時間復雜度。