聚類是一種將數據點按一定規則分群的機器學習技術。

給定一組數據點，我們可以使用聚類算法將每個數據點分類到一個特定的簇中。理論上，屬于同一類的數據點應具有相似的屬性或特征，而不同類中的數據點應具有差異很大的屬性或特征。

聚類屬于無監督學習中的一種方法，也是一種在許多領域中用于統計數據分析的常用技術。在數據科學中，我們可以使用聚類分析，來獲得一些有價值的信息。其手段是在應用聚類算法時，查看數據點會落入哪些類。

現在，我們來看看數據科學家們需要掌握的5種常見聚類算法以及它們的優缺點！　　▌K-均值聚類　　K-Means可能是最知名的聚類算法，沒有之一。在很多介紹性的數據科學和機器學習課程中，都有講授該算法。并且該算法的代碼很容易理解和實現！你可以通過看下面的插圖來理解它。

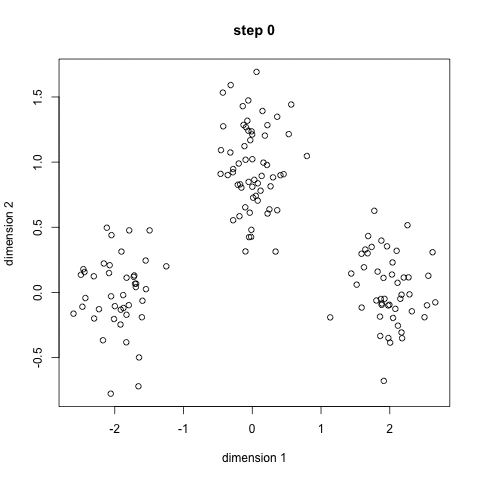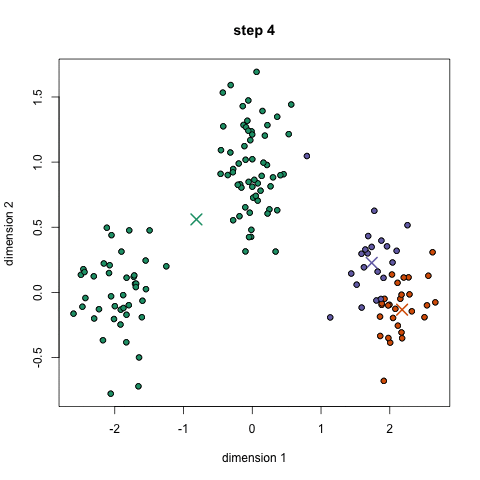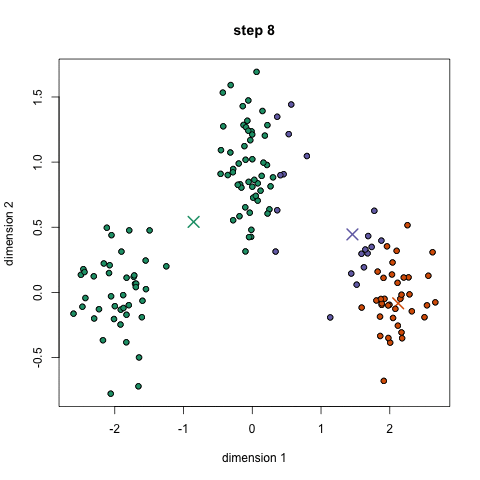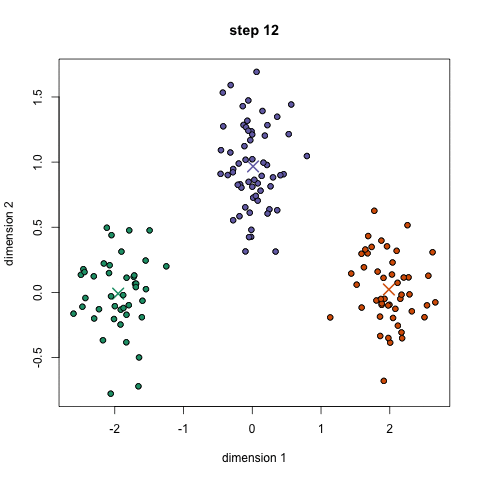
K均值聚類

1、首先，我們選擇一些要使用的類/組，并隨機初始化他們各自的中心點（質心）。要計算出簇（類）的使用數量，最好的方法是快速查看一下數據并嘗試鑒別有多少不同的分組。中心點是一個矢量，它到每個數據點的矢量長度相同，在上圖中用“X”來表示。　　2、每個數據點通過計算該點與每個簇中心之間的距離來進行分類，根據最小距離，將該點分類到對應中心點的簇中。　　3、根據這些已分類的點，我們重新計算簇中所有向量的均值，來確定新的中心點。　　4、重復以上步驟來進行一定數量的迭代，或者直到簇中心點在迭代之間變化不大。你也可以選擇多次隨機初始化簇中心點，然后選擇看起來像是最佳結果的數據，再來重復以上步驟。　　K-Means算法的優勢在于它的速度非常快，因為我們所做的只是計算點和簇中心之間的距離; 這已經是非常少的計算了！因此它具有線性的復雜度O(n)。　　但是，K-Means算法也是有一些缺點。首先，你必須手動選擇有多少簇。

這是一個很大的弊端，理想情況下，我們是希望能使用一個聚類算法來幫助我們找出有多少簇，因為聚類算法的目的就是從數據中來獲得一些有用信息。

K-means算法的另一個缺點是從隨機選擇的簇中心點開始運行，這導致每一次運行該算法可能產生不同的聚類結果。

因此，該算法結果可能具有不可重復，缺乏一致性等性質。而其他聚類算法的結果則會顯得更一致一些。　　K-Medians是與K-Means類似的另一種聚類算法，它是通過計算類中所有向量的中值，而不是平均值，來確定簇的中心點。

這種方法的優點是對數據中的異常值不太敏感，但是在較大的數據集時進行聚類時，速度要慢得多，造成這種現象的原因是這種方法每次迭代時，都需要對數據進行排序。　　▌Mean-Shift聚類算法　　Mean-Shift是一種基于滑動窗口的聚類算法。也可以說它是一種基于質心的算法，這意思是它是通過計算滑動窗口中的均值來更新中心點的候選框，以此達到找到每個簇中心點的目的。然后在剩下的處理階段中，對這些候選窗口進行濾波以消除近似或重復的窗口，找到最終的中心點及其對應的簇。看看下面的圖解。

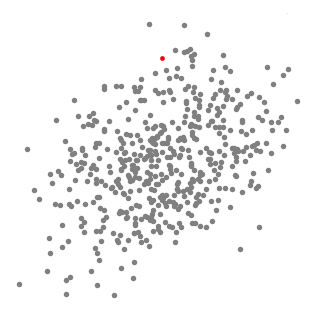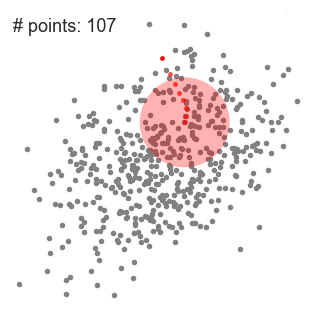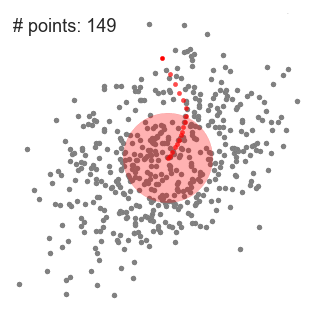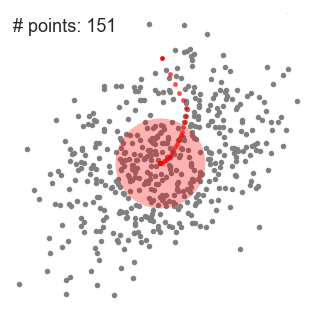
用于單個滑動窗口的Mean-Shift聚類算法

1、為了闡釋Mean-shift算法，我們可以考慮二維空間中的一組點，如上圖所示。我們從一個以C點（隨機選擇）為中心，以半徑r為核心的圓滑動窗口開始。Mean-shift可以看作是一種等高線算法，在每次迭代中，它能將核函數（圓滑動窗口）移動到每個迭代中較高密度的區域，直至收斂。　　2、在每次迭代中，通過將中心點移動到窗口內點的平均值處（因此得名），來使滑動窗口移向更高密度的區域。滑動窗口內的數據密度與其內部點的數目成正比。當然，通過移動窗口中點的平均值，它（滑動窗口）就會逐漸移向點密度更高的區域。　　3、我們繼續根據平均值來移動滑動窗口，直到不能找到一個移動方向，使滑動窗口可以容納更多的點。看看上面圖片的動畫效果；直到滑動窗口內不再增加密度（即窗口中的點數），我們才停止移動這個圓圈。　　4、步驟1至步驟3的過程是由許多滑動窗口來完成的，直到所有的點都能位于對應窗口內時才停止。當多個滑動窗口重疊時，該算法就保留包含最多點的窗口。最終所有數據點根據它們所在的滑動窗口來確定分到哪一類。　　下圖顯示了所有滑動窗口從頭到尾的整個移動過程。每個黑點代表滑動窗口的質心，每個灰點代表一個數據點。

Mean-Shift聚類的整個過程

與K-means聚類算法相比，Mean-shift算法是不需要選擇簇的數量，因為它是自動找尋有幾類。這是一個相比其他算法巨大的優點。而且該算法的聚類效果也是非常理想的，在自然數據驅動的情況下，它能非常直觀的展現和符合其意義。算法的缺點是固定了窗口大小/半徑“r”。　　▌基于密度的噪聲應用空間聚類（DBSCAN）　　DBSCAN是一種基于密度的聚類算法，類似于Mean-shift算法，但具有一些顯著的優點。我們從看下面這個奇特的圖形開始了解該算法。

DBSCAN笑臉人臉聚類

1、DBSCAN算法從一個未被訪問的任意的數據點開始。這個點的鄰域是用距離epsilon來定義（即該點ε距離范圍內的所有點都是鄰域點）。　　2、如果在該鄰域內有足夠數量的點（根據minPoints的值），則聚類過程開始，并且當前數據點成為新簇中的第一個點。否則，該點將被標記為噪聲（稍后，這個噪聲點可能成為聚類中的一部分）。在這兩種情況下，該點都會被標記為“已訪問”。　　3、對于新簇中的第一個點，它的ε距離鄰域內的點也會成為同簇的一部分。這個過程使ε鄰域內的所有點都屬于同一個簇，然后對才添加到簇中的所有新點重復上述過程。　　4、重復步驟2和3兩個過程直到確定了聚類中的所有點才停止，即訪問和標記了聚類的ε鄰域內的所有點。　　5、一旦我們完成了當前的聚類，就檢索和處理新的未訪問的點，就能進一步發現新的簇或者是噪聲。重復上述過程，直到所有點被標記為已訪問才停止。由于所有點已經被訪問完畢，每個點都被標記為屬于一個簇或是噪聲。　　與其他聚類算法相比，DBSCAN具有很多優點。首先，它根本不需要確定簇的數量。不同于Mean-shift算法，當數據點非常不同時，會將它們單純地引入簇中，DBSCAN能將異常值識別為噪聲。另外，它能夠很好地找到任意大小和任意形狀的簇。　　DBSCAN算法的主要缺點是，當數據簇密度不均勻時，它的效果不如其他算法好。這是因為當密度變化時，用于識別鄰近點的距離閾值ε和minPoints的設置將隨著簇而變化。在處理高維數據時也會出現這種缺點，因為難以估計距離閾值ε。　　▌使用高斯混合模型（GMM）的期望最大化（EM）聚類　　K-Means算法的主要缺點之一就是它對于聚類中心平均值的使用太單一。

通過查看下面的圖例，我們可以明白為什么它不是使用均值最佳的方式。

在左側，人眼看起來非常明顯的是，具有相同均值的數據中心點，卻是不同半徑長度的兩個圓形簇。

而K-Means算法不能解決這樣的數據問題，因為這些簇的均值是非常接近的。

K-Means算法在簇不是圓形的情況下也一樣無效，也是由于使用均值作為集群中心。

K-Means算法兩個失敗的案例

相較于K-means算法，高斯混合模型（GMMs）能處理更多的情況。對于GMM，我們假設數據點是高斯分布的; 這是一個限制較少的假設，而不是用均值來表示它們是圓形的。這樣，我們有兩個參數來描述簇的形狀：即均值和標準差！以二維為例，這意味著這些簇可以是任何類型的橢圓形（因為GMM在x和y方向上都有標準偏差）。因此，每個高斯分布都被單個簇所指定。　　為了找到每個簇的高斯參數（例如平均值和標準差），我們將使用期望最大化（EM）的優化算法。請看下面的圖表，可以作為匹配簇的高斯圖的闡釋。然后我們來完成使用GMM的期望最大化聚類過程。

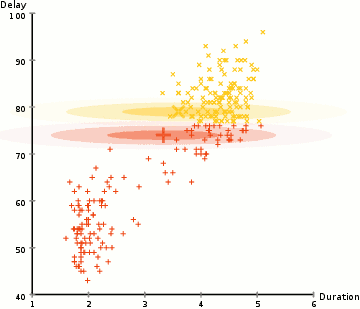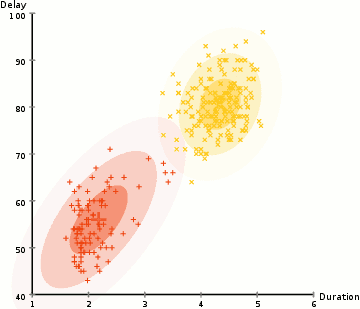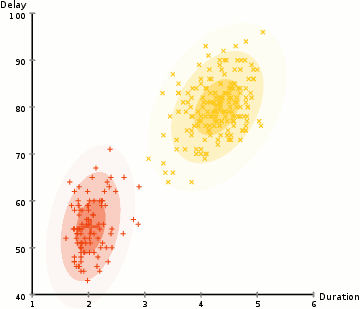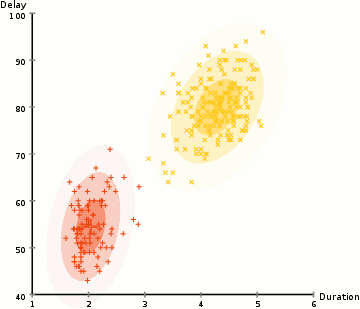
使用GMM的EM聚類

1、我們首先選擇簇的數量（如K-Means），然后隨機初始化每個簇的高斯分布參數。可以通過快速查看數據的方式，來嘗試為初始參數提供一個較好的猜測。不過請注意，從上圖可以看出，這不是100％必要的，因為即使是從一個很差的高斯分布開始，算法也能很快的優化它。　　2、給定每個簇的高斯分布，計算每個數據點屬于特定簇的概率。一個點越靠近高斯的中心，它越可能屬于該簇。在使用高斯分布時這應該是非常直觀的，因為我們假設大部分數據更靠近簇的中心。　　3、基于這些概率，我們為高斯分布計算一組新的參數，使得我們能最大化簇內數據點的概率。我們使用數據點位置的加權和來計算這些新參數，其中權重是數據點屬于該特定簇的概率。為了更直觀的解釋這個，我們可以看看上面的圖片，特別是黃色的簇。第一次迭代時，分布是隨機開始，但是我們可以看到大部分黃點都在分布的右側。當我們計算按概率加權的和時，即使中心附近的點大部分都在右邊，通過分配的均值自然就會接近這些點。我們也可以看到，大部分數據點都是“從右上到左下”。因此，改變標準差的值，可以找到一個更適合這些點的橢圓，以最大化概率加權的總和。　　4、重復迭步驟2和3，直到收斂，也就是分布在迭代中基本再無變化。　　使用GMM方法有兩個很重要的優點。 首先，GMM方法在聚類協方差上比K-Means靈活得多; 由于使用了標準偏差參數，簇可以呈現任何橢圓形狀，而不是被限制為圓形。 K-mean算法實際上是GMM的一個特殊情況，即每個簇的協方差在所有維度上都接近0。其次，由于GMM使用了概率，每個數據點可以有多個簇。因此，如果一個數據點位于兩個重疊的簇的中間，我們可以簡單地定義它的類，即屬于類1的概率是百分之X，屬于類2的概率是百分之Y。即，GMM支持混合類這種情況。　　▌凝聚層次聚類　　分層聚類算法實際上分為兩類：自上而下或自下而上。

自下而上的算法首先將每個數據點視為一個單一的簇，然后連續地合并（或聚合）成對的簇，直到所有的簇都合并成一個包含所有數據點的簇。

因此，自下而上的分層聚類被稱為合成聚類或HAC。

這個簇的層次可以用樹（或樹狀圖）表示。樹的根是收集所有樣本的唯一簇，葉是僅具有一個樣本的簇。

在進入算法步驟之前，請查看下面的圖解。

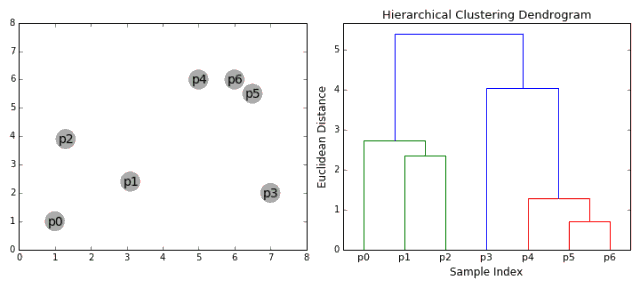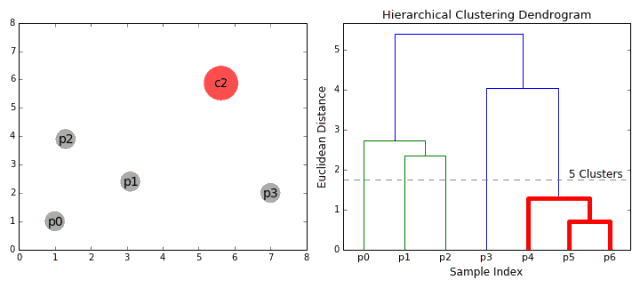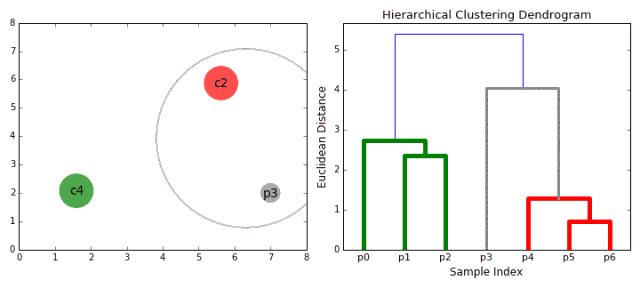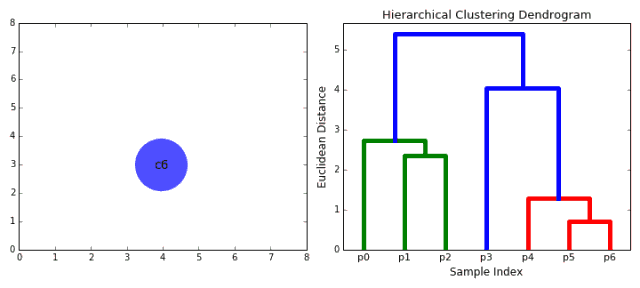
合成聚類

1、我們首先將每個數據點視為一個單一的簇，即如果我們的數據集中有X個數據點，那么我們就有X個簇。然后，我們選擇一個距離度量，來度量兩個簇之間距離。作為一個例子，我們將使用平均關聯度量，它將兩個簇之間的距離定義為第一個簇中的數據點與第二個簇中的數據點之間的平均距離。　　2、在每次迭代中，我們將兩個簇合并成一個簇。選擇平均關聯值最小的兩個簇進行合并。根據我們選擇的距離度量，這兩個簇之間的距離最小，因此是最相似的，所有應該合并。　　3、重復步驟2直到我們到達樹的根，即我們只有一個包含所有數據點的簇。通過這種方式，我們可以選擇最終需要多少個簇。方法就是選擇何時停止合并簇，即停止構建樹時！　　分層次聚類不需要我們指定簇的數量，我們甚至可以在構建樹的同時，選擇一個看起來效果最好的簇的數量。

另外，該算法對距離度量的選擇并不敏感；

與其他距離度量選擇很重要的聚類算法相比，該算法下的所有距離度量方法都表現得很好。

當基礎數據具有層次結構，并且想要恢復層次結構時，層次聚類算法能實現這一目標；

而其他聚類算法則不能做到這一點。

與K-Means和GMM的線性復雜性不同，層次聚類的這些優點是以較低的效率為代價，即它具有O（n3）的時間復雜度。